今回は、ダニエル・カーネマンの「少数の法則」について。
「アメリカにある3141の郡で腎臓ガンの出現率を調べたところ、顕著なパターンが発見された。出現率が低い郡の大半は、人口密度の低い田舎の農村部だったのだ」
このような統計結果を聞くと、僕たちはつい「田舎は水や空気がキレイで、添加物を使わない新鮮な食品が手に入るから、ガンを予防できるのだろうな」と結論づけてしまいがちです。
ただ、その一方で
「アメリカにある3141の郡で腎臓ガンの出現率を調べたところ、顕著なパターンが発見された。出現率が高い郡の大半は、人口密度の低い田舎の農村部だったのだ」
このような統計結果を聞くと、僕たちは「田舎は質の高い医療を受けにくいし、飲酒率や喫煙率が高いから、それがガンの原因になっているのだろうな」と結論づけてしまいがち。
しかし、「出現率が低い田舎には腎臓ガンを予防する何かがあるはずだ」という予想も「出現率が高い田舎には腎臓ガンの原因となる何かがあるはずだ」という予想も、外れかもしれません。
実は、ただ単に調査の対象となる人口が少ないことが原因で、こういった統計結果が得られる可能性があるのです。
というのも、統計データには「調査の対象となる数が少なければ少ないほど、単なる偶然によって極端な値をとりやすくなる」という性質があるからです。
試行回数が少ない方が偏った結果が起きやすい
偏りのないコインを10回投げて3回しか表が出ないことはあっても、100回投げて30回しか表が出ないことは滅多にありません。
同じように、偏りのないコインを100回投げて45回しか表が出ないことはあっても、1000回投げて450回しか表が出ないことは滅多にありません。

このように、試行回数 n が大きければ大きいほど「結果として得られる出現率」は「真の出現確率」から離れた値をとりにくくなっていくことを、大数の法則と言います。
この事実は、「真の出現確率」が予測しやすいものについてはスッと納得しやすい定理です。
実際、「10円玉を10回投げたら3回だけ表が出て、100円玉を100回投げたら45回表が出た」のに対して、10円玉の方が表が出にくいと思う人は少ないはずです。

その一方で、これが「人口100000人のX市では4%の人に起きて、人口1000人のZ村では3%の人に起きた現象」となると、それを偶然とは考えずに「Z村では出現確率が0.75倍に下がる」と考えてしまいますよね。
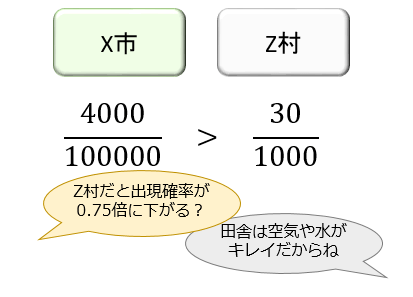
しかし、「真の出現確率が4%の現象が1000人中30人以下にしか起きない確率」は約5.8%。
たとえ本質的な差が全くなかったとしても、同じくらいの規模の村が17もあれば1村くらいはある程度の誤差の範囲内なのです。
このように「試行回数(サンプルサイズ)n が小さければ小さいほど、それだけ全くの偶然だけでも極端な値をとりやすいにも関わらず、そこに大数の法則が当てはまると錯覚し、真に差があると誤解してしまうこと」を、行動経済学で有名な心理学者ダニエル・カーネマンは少数の法則と呼んでいます。
ただ、ポアソンの極限定理は大数の法則とは関係がないので、ダニエル・カーネマンの意味のほうがしっくり来ますね。
統計データを見るときは「どれだけの人数について調査したか」に注意を向け、もし何らかのランキングの極端な上位・下位がどれも数の少ないグループだった場合には、「何か秘訣があるはずだ」と考える前に「少数の法則の可能性はないかな?」と考えてみてください。
もちろん、本当に何か秘訣があって1位を取った可能性も十分あります。
しかし、実際には本質的な差がなかったとしても、ただ「サンプルサイズが小さい」というだけで極端な上位や下位に入り込む可能性が相対的に高くなるという統計的事実を覚えておくと、統計にだまされにくくなるのは間違いありません。
案外、「出現率が極端に低い田舎」よりも「出現率がそこそこに低い地方都市」にこそ、病気になりにくい秘訣があるかもしれませんよ。