統計学の中でも特に頭を悩ませることの多い「p値(有意確率)」と「有意水準」。
有意水準は「ある仮説を否定した判断が誤りである確率 \(P(H_0|reject)\) 」と誤解されがちですが、実際には両者は大きく異なる値です。
有意水準は第一種の過誤確率、つまり「帰無仮説が正しい場合に、誤って帰無仮説を棄却(否定)してしまう確率 \(P(reject|H_0)\) 」を意味します。
有意水準5%とは仮説が正しい場合にこの手順を多数回実施して検定を行うとき、間違って帰無仮説を棄却する割合が5%であるという意味であり、特定の判断が間違っている確率が5%ということではない。
出典:改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎
(東京図書)p144
かなりややこしい部分のため、誤解されることも少なくない用語ですが、統計的仮説検定を行う上で非常に重要な存在です。
今回は、そんなp値(有意確率)と有意水準について解説していきます。
photo credit:Chris Potter
帰無仮説と統計量と実現値
p値と有意水準の説明をする前に、いくつか知っておくべき統計用語があるので、まずはそこから見ていきましょう。
今回の話は「このコイン、偏りのあるイカサマコインなのでは?検定で調べてみよう」
⇒「コインを10回投げたら2回しか表が出なかった」
という例で考えると分かりやすいです。
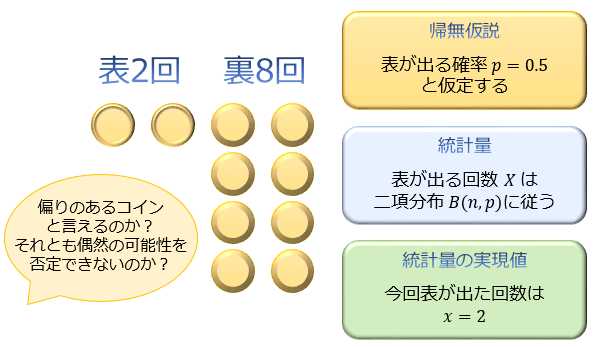
①帰無仮説:棄却(否定)されることを目的に立てられる仮説のこと。\(H_0\) と表記されます。
上の例では「このコインは偏りのないコインであり、表が出る確率は \(50\)% である」という仮説が帰無仮説になります。
「偏りのないコインである」という仮説を否定するだけの根拠を明示することで、「偏りのあるイカサマコインだ」と主張したい、ということですね。
②統計量:標本データから目的に応じて計算される「データの特徴を表す確率変数」のこと。
統計量は試行のたびに値が変動する確率変数であり、大文字のアルファベットで表されます。
検定に使うことを明示するために「検定統計量」と書くこともあります。
上の例では「コインを \(n=10\) 回投げたときに表が出る回数 \(X\)」が統計量です。帰無仮説の下では \(n=10 , p = 0.5\) より \(X\) は二項分布 \(B(10,0.5)\) に従います。
③統計量の実現値:得られた標本から計算して求められた「統計量が実際に取る値」のこと。
実現値は確定した値なので、試行のたびに色々な値をとる可能性のある統計量 \(X\) とは区別され、\(x\) と表記されます。
このように統計量に対応する小文字のアルファベットで表されることが多いです。
上の例では「コインを10回投げたら2回しか表が出なかった」という結果が得られていることから、\(x=2\) となります。
p値とは?有意水準とは?
それでは、本題です。
帰無仮説が正しいという条件の下で、今回得られた「統計量の実現値」以上に極端な「統計量」が観測される確率のことを、p値(有意確率)と言います。
「その仮説が正しいと仮定したら、今回みたいな結果が起きる確率はこんなにも低いんだ。偶然こんなに低い確率を引いたと考えるより、その仮説は正しくないと考える方が自然じゃない?」と主張するときの『こんなに低い確率』のことです。
p値が小さければ小さいほど、帰無仮説が正しくないと主張するのに強力な根拠となります。
例)p値が \(0.0002\) と求まった。つまり帰無仮説が正しければ、今回起きたような現象は \(0.02\)% の確率でしか起きない現象という事になる。偶然 \(0.02\)% を引いたとは考えにくい以上、帰無仮説は正しくないといわざるを得ない。
ただ、どれだけp値が小さくても「偶然 \(0.02\)% の確率を引いたのかも」と言われてしまうと何も主張できなくなってしまいますよね。
そこで、データを取る前には「p値がこの値より小さければ帰無仮説を棄却(否定)する基準」が設定されます。これが有意水準です。
有意水準は \(5\)% か \(1\)% に設定されることが多いです。
統計的検定の主な流れは、以下の通りになります。
①:帰無仮説(否定したい仮説)\(H_0\) を決める
②:検定に使う統計量を選択し、有意水準を設定する
③:実際にデータを取り、統計量の実現値を計算する
④:仮説の下では今回の統計量の実現値が珍しい値なのかどうかを調べる(p値の算出)
⑤-1:帰無仮説の下で偶然得られたと考えてもおかしくない値だと分かった場合、帰無仮説は棄却されない(帰無仮説が正しくないとは断定できない=何も言えない)
⑤-2:帰無仮説の下で偶然得られたとは考えにくいほど珍しい値だと分かった場合、帰無仮説を棄却する(帰無仮説が正しくないと判断する)
イメージとしては、背理法に近いですね。
注意点としては、仮説や有意水準はデータを取る前に決めておかなければならないこと。
いくら極端な結果でも、何回もデータを取ればいつかは出るものなので、極端な結果が出てから仮説や有意水準を決めてもそれは意味の薄い検定となります。
具体例から分かるp値
では実際に、具体例を通じて検定を行ってみましょう。
「このコイン、偏りのあるイカサマコインなのでは?統計的検定で調べてみよう」
①:帰無仮説(否定したい仮説)は「\(H_0\) :表が出る確率 \(p=0.5\)」
②:検定に使う統計量は \(10\) 回投げて表が出る回数 \(X\) 。有意水準は \(5\)% で両側検定(後述)する
③:実際にデータを取ったところ、統計量の実現値は \(x=2\) となった

④:帰無仮説の下で今回得られた統計量の実現値 \(x=2\) 以上に極端な統計量 \(X\) が得られる確率(p値)を求める
今回は「表が2回しか出なかった」わけですが、今回の結果以上に「\(p=0.5\) ではない」と主張できそうな極端な統計量としては「表が1回以下しか出ない」が挙げられます。
また、「表が8回以上出る」という場合も同じくらい「\(p=0.5\)」を否定する根拠になりうる極端な統計量と言えます。
このように、統計量の標本分布(下のグラフ)の両すそ部分をp値に含める検定を両側検定と言います。(片方の裾だけをp値に含める検定を片側検定と言います)
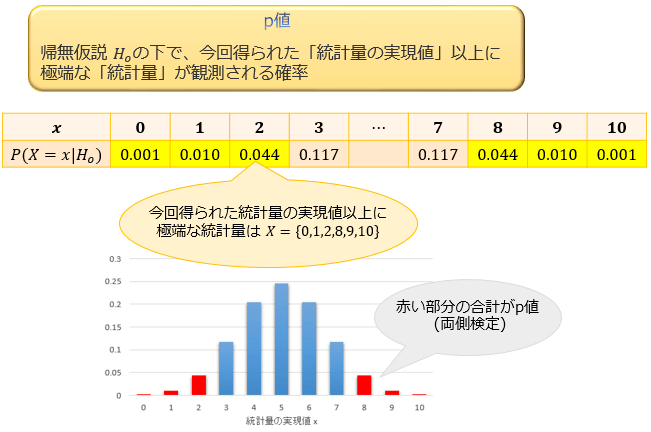
よって、\(X\) が二項分布 \(B(10,0.5)\) に従うという帰無仮説の下で今回得られた統計量の実現値 \(x=2\) 以上に極端な統計量 \(X\) が得られる確率(p値)は
\(P(X≤2|H_0)+P(X≥8|H_0)\)\(≒0.001+0.010+0.044+0.044+0.010+0.001=0.11\)
となります。
つまり、偏りのないコインだった場合でも「コインを10回投げたら2回しか表が出なかった」以上に極端な統計量が得られる確率は \(11\)% もあったということが分かります。
⑤-1:今回の有意水準は \(5\)% 、つまり \(0.05\) ですから、今回得られたp値 \((0.11)\) は有意水準 \((0.05)\) よりも大きな値ということになります。
すなわち、「コインを10回投げたら2回しか表が出なかった」という結果は「帰無仮説の下で偶然得られたと考えてもおかしくない値である」という結論になり、「このコインは偏りのないコインであり、表が出る確率は \(50\)% である」という帰無仮説は棄却されないことになります。
今回の結果はイカサマコインだ!と主張するのに十分な根拠にはならない、ということです。
注意してほしいのが、帰無仮説が棄却されない場合でも帰無仮説が正しいという結論にはならないということ。つまり「偏りのないコインだ」とも主張できないのです。帰無仮説が棄却されなかった場合はどちらとも言えない(データの数が足りない)が答えとなります。
帰無仮説が棄却されるケース
ちなみに、今回得られた結果が「コインを10回投げたら1回しか表が出なかった」である場合には、p値は \(0.022(< 0.05)\) となり、有意水準 \(5\)% で帰無仮説が棄却されます。
(「有意差がある」と表現されることもあります)
⑤-2:「偏りのないコインなのに、偶然1回しか表が出なかった」とは考えにくいことから、統計学的に見て「このコインは偏りのあるイカサマコインであると考えられる」と主張できるだけの合理的な根拠がある、ということになります。
×(よくある間違い)「このコインは、\(95\)% の確率で偏りのあるコインだ」
→この検定は \(P(H_0|D)\) を計算するものではありません。有意水準は \(P(reject|H_0)\) です。\(P(H_0|D)\) を計算するには情報が足りません。
◎(正しい)「このコインが偏りのないコインと仮定したら、今回のような極端な結果が得られる確率は \(5\)% 未満。偶然こんなに低い確率を引いたとは考えにくいことから、このコインが偏りのあるコインであると考えることには一定の合理性がある」
さらに理解を深めたいと思った方は、ぜひ以下の参考文献もご参照ください。
【参考文献】
1)山田剛史教授,村井潤一郎教授著『よくわかる心理統計』(ミネルヴァ書房)
2)浜田知久馬教授著『学会・論文発表のための統計学』(真興交易)
3)改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎(東京図書)