最小公倍数って何？その求め方と素因数分解のテクニック

このページでは、「最小公倍数」の意味・計算方法とカンタンに求めるテクニックについて書いていきます。

最小公倍数って何？

最小公倍数とは、「2つ以上の正の整数に共通する倍数のうち、一番小さな数」のこと。

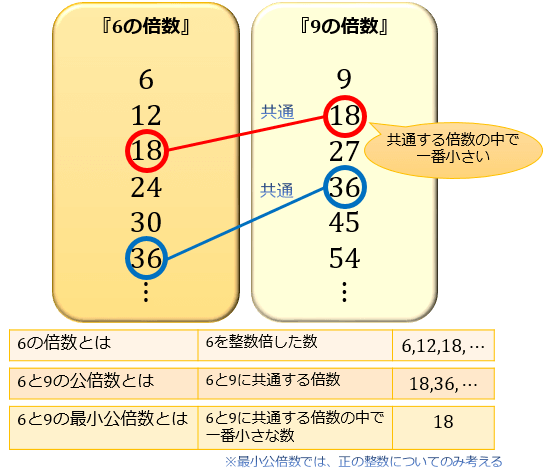
2つの数をそれぞれ1倍・2倍・3倍とかけ算していくと、下図のようにそれぞれの倍数の中には必ず共通する倍数が何個も出てくることが分かりますよね。

この「共通する倍数」のことを公倍数と言います。

そして、公倍数の中で最小のものを最小公倍数と言います。

具体的に、『 \(24\) と \(36\) の最小公倍数』を求め方をみていきましょう。

Tooda Yuuto

初めは「やり方①」、慣れてきたら「やり方②・③」がオススメです。

まずは、2つの数の倍数を書き並べる方法。

『 \(24\) と \(36\) の最小公倍数』を求めるために『 \(24\) の倍数』と『 \(36\) の倍数』を書き並べてみましょう。

たくさん書き並べたら、2つの倍数に共通する数を探します。

共通する倍数が、「 \(72,144,\cdots\) 」と見つかりました。

最小公倍数とは「共通する倍数の中で一番小さな数」でしたよね。

ここから、『 \(24\) と \(36\) の最小公倍数』は \(72\) と求まります。

次に、共通して割れる数で割っていく方法。

まず、下図のように2つの数を並べて書きます。

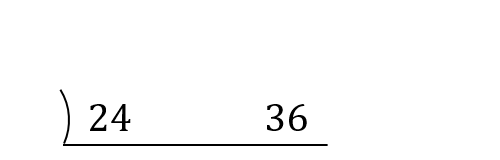
次に、この2つの数を共通して割れる数を考えましょう。

まず、\(24\) も \(36\) も \(2\) で割れますよね。

そしたら \(2\) を左に書いて、「 \(2\) で割り算した答え」を下に書いていきます。

「 \(24÷2=12\) 」「 \(36÷2=18\) 」なので、\(12\) と \(18\) を並べて書きましょう。

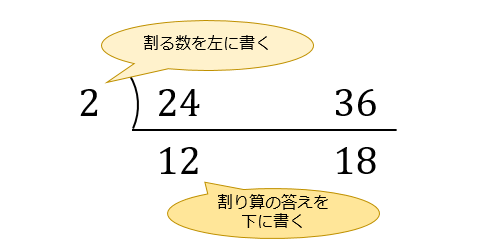
これを「共通して割れる数」がなくなるまで続けると、以下のようになります。

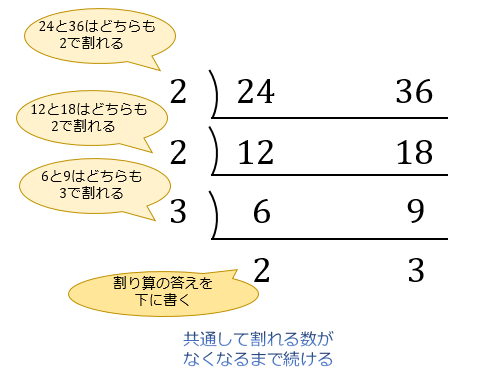
共通して割れる数がなくなったら、筆算の外側の数字を全部かけ算すると、最小公倍数が求まります。

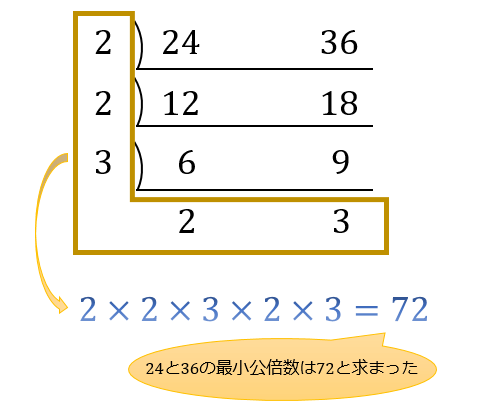
今回は、筆算の外側の数字が「 \(2,2,3,2,3\) 」なので「 \(2×2×3×2×3=72\) 」より、『 \(24\) と \(36\) の最小公倍数』は \(72\) と求まります。

最後は、素因数分解を利用するテクニックです。

Tooda Yuuto

素因数分解とは「 \(24=2×2×2×3\) 」のように素数のかけ算に分解する手法です。

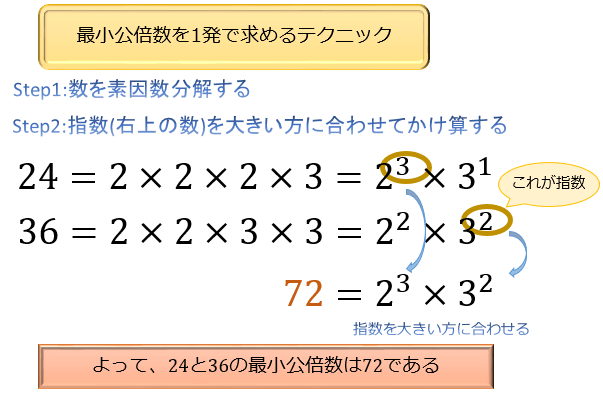
このテクニックを使えば、大きな2つの数の最小公倍数もスパッと求められるようになりますよ。