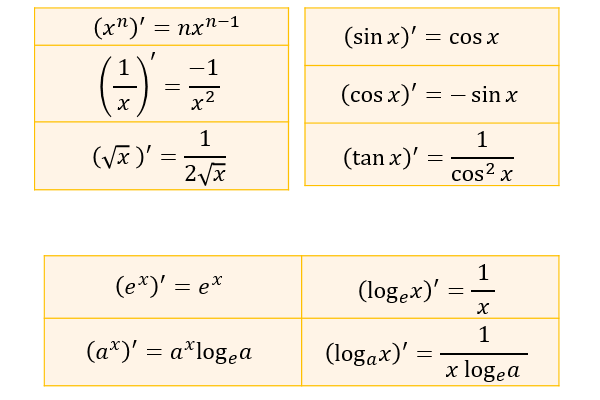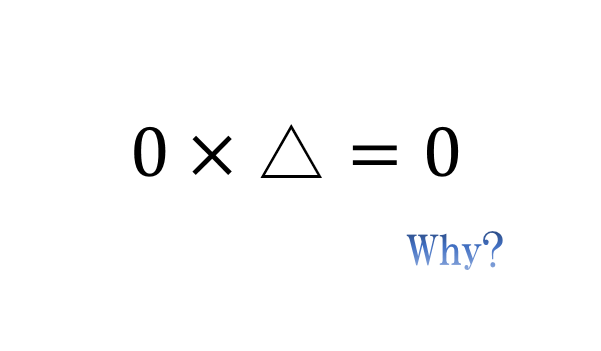
無いことを表す数、「0」。
0という概念を数として認めたことで、数学は飛躍的な進歩を遂げました。
ゼロは、数の中でも非常に特殊な性質をもっています。
それは0のかけ算。つまり「何に0をかけても0になり、0に何をかけても0になる」ことです。
△×0=0
0×△=0
しかし、「無い」数のかけ算とは不可解なものです。
無いものをどうやってかけるのか、疑問が湧いてくる方も多いのではないでしょうか。
そこで今回は、0のかけ算のイメージとその利便性について書いていこうと思います。
0の定義
0は、何もないことを表す数であり、1の直前の整数です。

「1に0を足す」ことは、「1に何もないを足す」⇒「1に何も足さない」ことを意味します。
何も足さないのですから、1は1のまま。
そのため、1+0=1となります。
0のかけ算のイメージ
では、0のかけ算は一体何を意味しているのでしょうか。
「何もない」をかける、では意味がよく分かりません。
そこで「2×3=6」「2×0=0」「0×3=0」の3つの視点から具体的にイメージしてみましょう。
「2×3=6」
「いま、机の上には水が2ℓ入ったビンが3本あります。このとき、机の上に水は全部で何リットルあるでしょうか?」
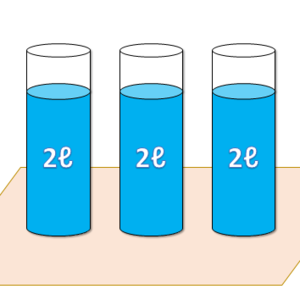
これが、2×3=6です。
「2×0=0」
「いま、机の上には水が2ℓ入ったビンが0本あります(=1本もありません)。このとき、机の上に水は全部で何リットルあるでしょうか?」
これが、2×0=0です。
水が2ℓ入ったビンが机の上から無くなる=0本になると、机の上にある水は0ℓになりますよね。
これが「0をかけると0になる」理由です。
「0×3=0」
「いま、机の上には空(=水が0ℓ)のビンが3本あります。このとき、机の上に水は全部で何リットルあるでしょうか?」
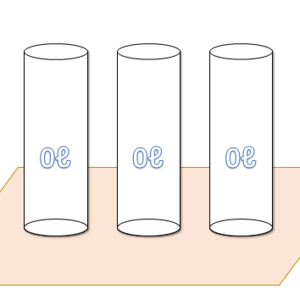
これが、0×3=0です。
水が0ℓ入ったビンが机の上にどれだけあろうと、机の上にある水は0ℓから変わりません。
これが「0に何をかけても0になる」理由です。
上の3つの例を見比べると、0のかけ算のイメージがついたのではないでしょうか。
0のかけ算の便利なところ
0のかけ算の存在は、「0×2+1×1+2×0+3×2=?」といったようにかけ算と足し算が組み合わさったときに便利になってきます。
身近な例だと、商品の集計がこれに当たります。
たとえば「水〇ℓ入りのビンがそれぞれ何本あるか」から、「ビンが合計何本あって、水が合計何ℓあるか」を集計したい場合。

商品の数は、毎日変動します。
今日はたまたま2ℓ入りのビンがありませんでしたが、明日の仕入れで入ってくるかもしれません。
また、今ある3ℓ入りのビンは明日にはないかもしれません。
ここで、いちいち「今日は2ℓ入りのビンがないから、1×1+3×2=7ℓだな。で、ビンの数を計算するときは0ℓのビンも集計するから…」と判断するのは非効率です。
商品の種類が少ないならまだ良いですが、商品の種類が100種を超えてくると非常に面倒になってきますよね。
そんなときに役に立つのが0のかけ算です。

0のかけ算を利用すると、Excelで上のような表を作ることができます。
Dの列に各商品の数量を入力するだけで、0本だろうと0ℓビンだろうと関係なく計算し、「ビンが合計何本あって、水が合計何ℓあるか」を算出できるようになるんです。
緑のセルの数字が7なので、水は合計7ℓとなります。
商品の種類が増えれば増えるほど、0のかけ算の存在による計算の利便性は高まっていきます。
物が大量に増えた現代において、0のかけ算の存在は私たちの生活に欠かせないものとなっているのです。
まとめ
①0は何もないことを表す数であり、1の直前の整数である。
②水が2ℓ入ったビンが机の上から無くなると、机の上にある水も0ℓになる。これが0をかけると0になる理由。
③水が0ℓ入ったビンが机の上にどれだけあろうと、机の上にある水は0ℓ。これが0に何をかけても0になる理由。
④0のかけ算が本領を発揮するのは、かけ算と足し算が組み合わさったとき。身近な例だと商品を集計するときに便利。
「0とかけ算の関係」の次は、「0と割り算の関係」についてです。
次のページでは、「なぜゼロで割ってはいけないのか?」を見ていきましょう。