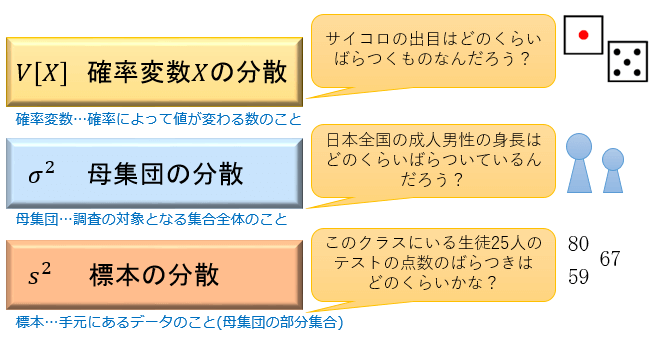
中央値(メジアン)とは、データを大きさの順に並べたときに全体の中央に位置する値のことです。
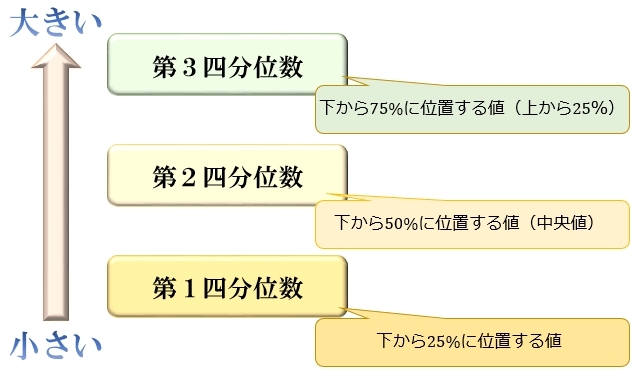
同じく、データを大きさの順に並べたときに下から25%に位置する値・50%に位置する値・75%に位置する値のことを第1四分位数・第2四分位数・第3四分位数と言います。
中央値は英語でMedian、四分位数の読み方は「しぶんいすう」で英語ではQuartileと言います。
中央値や四分位数の求め方は、データの数が偶数個か奇数個かによって少し変わってきます。
特に四分位数の求め方には複数の流儀があり、混乱しやすいです。
試験ではヒンジと呼ばれる簡易的な四分位数が問われることが多いので、そちらの求め方をじっくりと見ていきましょう。
中央値(メジアン)の求め方
中央値は、以下の3つのステップから求められます。
- データを小さい順に並べる
- データの数が「奇数個 or 偶数個」のどちらなのか調べる
- 奇数個ならちょうど真ん中の数、偶数個なら真ん中の2つの数の平均値を調べる
データの数が奇数個の場合
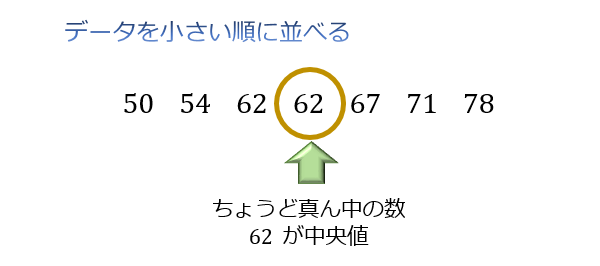
データが奇数個の場合は「小さい順に並べたときに真ん中に来る数」が中央値となります。
問題1:7個のデータ \(62,67,78,50,62,54,71\) の中央値を求めて下さい。
データの数が偶数個の場合
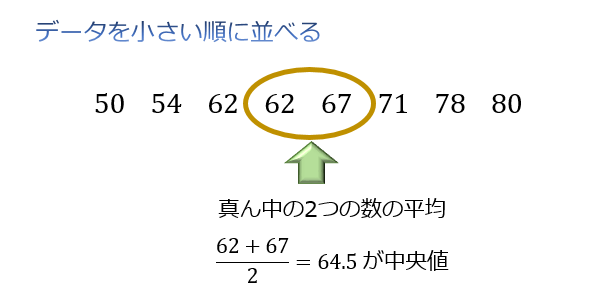
データが偶数個の場合は「小さい順に並べたときに真ん中に来る2つの数の平均値」が中央値となります。
問題2:8個のデータ \(62,67,78,50,62,80,54,71\) の中央値を求めて下さい。
平均値・中央値・最頻値の使い分け方やそれぞれのメリットとデメリットについては、以下の記事で詳しく解説しているので参考にしてみてください。
四分位数(ヒンジ)の求め方
四分位数の求め方には複数の流儀がありますが、高校の数学Ⅰで教えられている四分位数(ヒンジ)の求め方は以下の通りです。
- データを小さい順に並べる
- 中央値を求める(第2四分位数)
- 中央値より小さい「前半データ」と中央値より大きい「後半データ」に分ける
- 前半データ内での中央値が第1四分位数、後半データ内での中央値が第3四分位数
- 第3四分位数から第1四分位数を引いた値を四分位範囲という
- 四分位範囲の \(1/2\) 倍を四分位偏差という
文字だけだと「分かりにくい…」と感じる方も多いのではないでしょうか。
でも大丈夫。四分位数は、図にして考えると一気に分かりやすくなります。
いくつか具体例を見ていきましょう。
問題3:11個のデータ \(50,54,62,62,67,71,78,80,82,86,87\) の四分位偏差を求めて下さい。
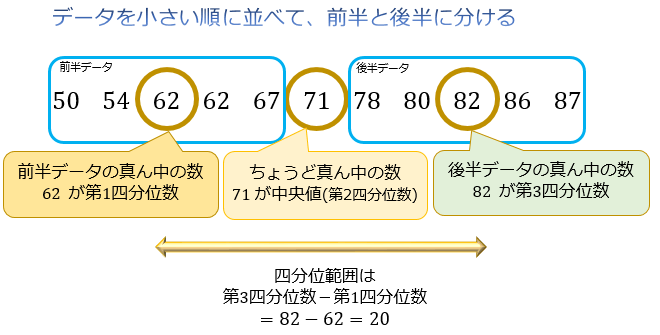
四分位偏差は \(20×1/2=10\) となります。
問題4:10個のデータ \(50,54,62,62,67,71,78,80,82,86\) の四分位偏差を求めて下さい。
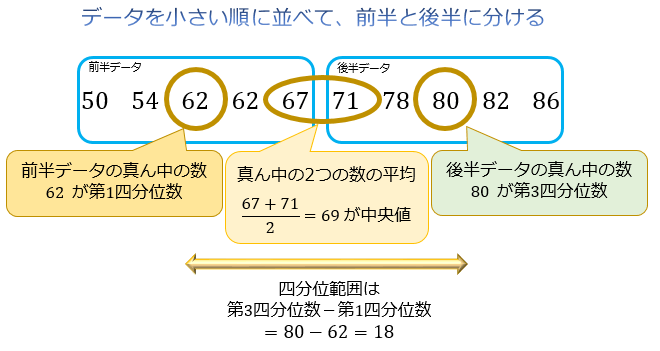
四分位偏差は \(18×1/2=9\) となります。
問題5:9個のデータ \(50,54,62,62,67,71,78,80,82\) の四分位偏差を求めて下さい。
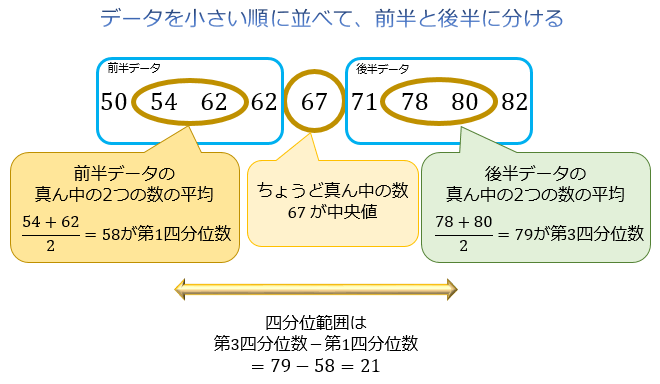
四分位偏差は \(21×1/2=10.5\) となります。
問題6:8個のデータ \(50,54,62,62,67,71,78,80\) の四分位偏差を求めて下さい。
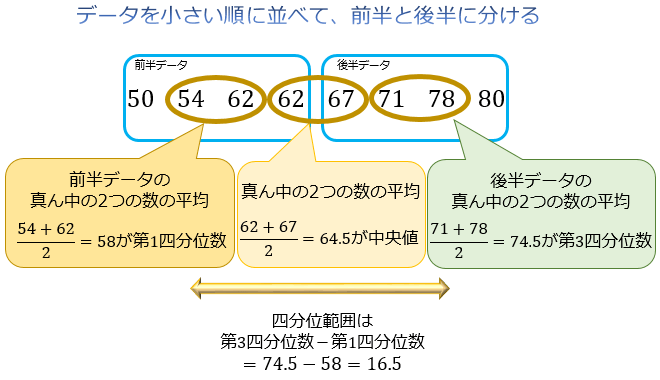
四分位偏差は \(16.5×1/2=8.25\) となります。
四分位範囲・四分位偏差とは
第3四分位数から第1四分位数を引いた値を四分位範囲
第3四分位数から第1四分位数を引いた値の \(1/2\) 倍を四分位偏差と言います。
四分位範囲と四分位偏差は、どちらもデータのばらつきの大きさ(散らばり具合)を表す指標です。
似たような指標として標準偏差がありますが、四分位範囲・四分位偏差は標準偏差と比べて①計算が簡単②外れ値(極端な値)に引っ張られにくいというメリットがあります。
反対に、標準偏差には正規分布において68%95%ルールが成立するという大きなメリットがあります。(詳しくは下記記事を参照)

状況に応じて使い分けていきましょう。
Excelの厳密な四分位数(Quartile関数)の求め方
Excelで四分位数を求める関数としてはQuartile関数があります。
Quartile関数は厳密な25%点・75%点を求める関数のため、さきほどの簡易的な四分位数(ヒンジ)とは若干異なる値が出てくる点に注意が必要です。
例えば、10個のデータ \(1,2,3,4,5,6,7,8,9,10\) の第3四分位数を求める場合、先ほどの求め方だと \(8\) になるはずですが、Quartile関数だと \(7.75\) という答えが返ってきます。(中央値は同じ答え)

このExcelの厳密な四分位数(Quartile関数)の求め方はさきほどのヒンジとは若干異なり、以下の手順を踏みます。
- データを小さい順に並べる
- 「データの個数から \(1\) を引いた値」に25%、50%、75%をかける
- 答えが整数 \(k\) なら \(k+1\) 番目の数が四分位数
- 答えが \(k+0.25\) なら \(k+1\) 番目の \(0.75\) 倍と \(k+2\) 番目の \(0.25\) 倍の合計が四分位数
- 答えが \(k+0.5\) なら \(k+1\) 番目の \(0.5\) 倍と \(k+2\) 番目の \(0.5\) 倍の合計が四分位数
- 答えが \(k+0.75\) なら \(k+1\) 番目の \(0.25\) 倍と \(k+2\) 番目の \(0.75\) 倍の合計が四分位数
Excelを使って計算するときに「こういう理屈で求まっているんだな」くらいにおさえておいてください。