ベイズ推定とは、観測された事実から推定したい事柄を確率的に推定する手法の1つです。
→「あの学校は男子校である確率が高いな。共学の確率もまだ0ではないけど」
ベイズ推定は、統計感覚を身に着けるうえで絶対に学ぶ必要のある理論です。
しかし同時に、ベイズ推定は非常に誤解されやすい理論でもあります。
今回は、そんなベイズ推定にまつわる4パターンについて解説していきます。
photo credit:Marcus Hansson
前提条件
前提①Aさん・Bさん・Cさん・Dさんにはそれぞれ子供が2人いる。双子はいない
前提②各親には、子供の性別の組み合わせが(男,男)(男,女)(女,男)(女,女)の4パターンあり、それぞれの存在確率は同じ(25%)とする。
前提③誰も嘘をつかない
と仮定します。
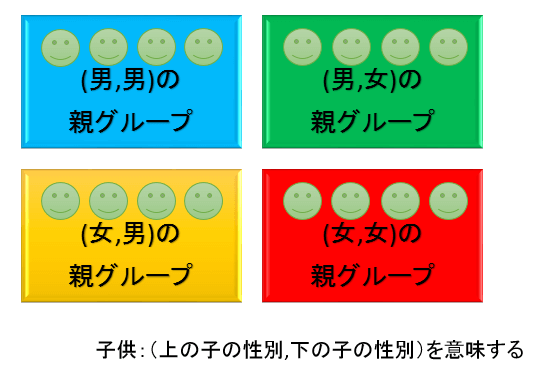
今回取り上げるベイズ推定では、4つの「子供の性別の組み合わせ」の親が各4人ずつの合計16人いると考えると分かりやすくなります。
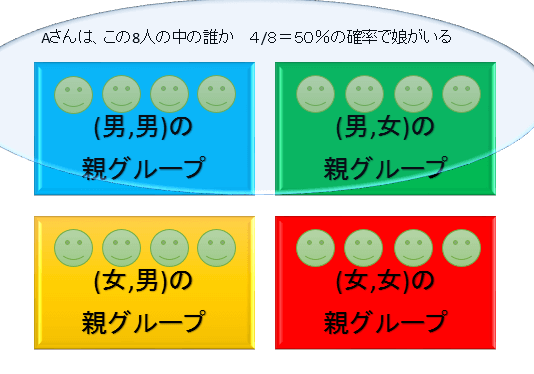
(1)Aさんの上の子が男の子だと分かった。この時、Aさんの下の子が女の子である確率は?
Aさんの上の子が男の子だと分かった。この時、Aさんの下の子が女の子である確率は何%でしょうか?
前提②のうち、上の子が男の子であるパターンは(男,男)(男,女)の2パターンで、その存在確率は同じ(=50%)です。
そのため、下の子が女の子である確率=(男,女)の存在確率=50%となります。
これは問題ないはず。
答え:50%
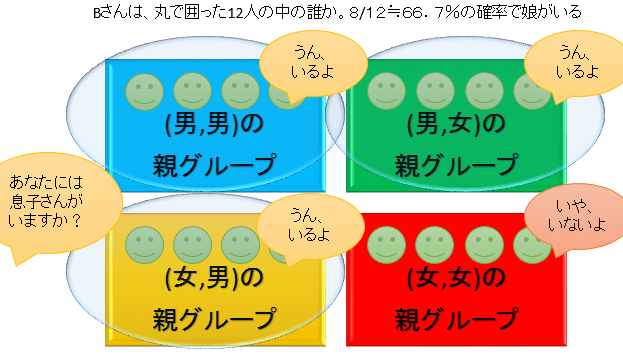
(2)「Bさんって息子さんいましたっけ?」とBさんに聞いたら「うん、いるよ」と答えた。この時、Bさんに娘がいる確率は?
「Bさんって息子さんいましたっけ?」とBさんに聞いたら「うん、いるよ」と答えた。この時、Bさんに娘がいる確率は何%でしょうか?
この場合、答えは1/2にはなりません。2/3になります。
前提②より子供2人の性別の組み合わせは(男,男)(男,女)(女,男)(女,女)の4パターンで、それぞれの存在確率は同じ(=25%)です。
このうち、「Bさんって息子さんいましたっけ?」という質問に「うん、いるよ」と答えるのは(男,男)(男,女)(女,男)の3パターンで、その存在確率は同じ(=33.33…%)。
そのため、Bさんに娘がいる確率=(男,女)の存在確率+(女,男)の存在確率=66.66…%となります。
「ある子が男の子か女の子かの確率は50%でも、条件が加わると確率が変わる」
これがベイズ推定の重要なポイントです。
答え:2/3=約66.7%
(3)「Cさん、お子さんの写真を見せてもらえませんか?」とCさんに尋ねたら息子さんが写った写真を見せてもらえた。この時、Cさんに娘がいる確率は?
「Cさん、お子さんの写真を見せてもらえませんか?」とCさんに尋ねたら息子さんが写った写真を見せてもらえた。この時、Cさんに娘がいる確率は何%でしょうか?
「あ、これはさっきと同じ問題だ。2/3でしょ?」と思ったあなたは要注意。
この問題の場合は、答えは1/2(=50%)と推定できます。
「え!?(2)と何が違うの?」と思うかもしれませんが、実は大きな違いがあるんです。
それは存在確率の差です。
(2)では、Bさんに娘がいようと息子が1人でもいれば必ず「うん、いるよ」と答えます。
しかし(3)では、Cさんに娘がいたら「Cさんは娘さんの写真を見せたかもしれない」という可能性が出てくるんです。
どちらの子供の写真を見せるかは50%と考えられるので、(男,女)(女,男)の2パターンの存在確率はそれぞれ(男,男)の存在確率の半分と推定できます。
そのため、Cさんに娘がいる確率=(男,女)の存在確率+(女,男)の存在確率=50%と推定できるんです。

「推定」なのは、もし日本に「息子1人・娘1人の場合に子供の写真を見せてと頼まれたら、絶対に息子の写真を見せる」という文化があったなら、(2)と同じ現象になり、娘がいる確率は2/3となるからです。
反対に、Cさんが前に「女の子の写真を見せた方が喜ばれると思う」と発言していたなら、娘がいる確率は1/2よりもかなり低い確率だと推定できます。
(女の子の写真を見せた方が良いと考えているのに、息子の写真を見せた=どちらも男の子である可能性が高い)
いずれにしても、情報が事後確率を変動させていることに変わりはありません。
ただ、今回は「子供が2人いるCさんに子供の写真を見せてほしいといったら、息子の写真をみせてもらえた」以外に情報がないので、娘がいる確率は50%と推定されます。
なんとなく、ベイズ推定の仕組みが分かってきたのではないでしょうか?
答え:50%と推定できる
(4)Dさんには少なくとも息子が1人いることが分かった。この時、Dさんに娘がいる確率は?
さて、ここでタイトル回収。
Dさんには少なくとも息子が1人いることが分かった。この時、Dさんに娘がいる確率は何%でしょうか?
この問題の答え、分かりますか?
ぼくには分かりません。
数学的に考えると「少なくとも息子が1人いる」という情報は(2)と同じと考えられ、2/3という答えが出てきそうです。
しかし、本当にそうでしょうか?
一般的に、「息子さんが1人だけ写っている写真を見た」や「電話をかけたら息子さんが出た」といった情報を得た場合も日本語では「少なくとも息子が1人いることが分かった」と表現されます。
そして、これらは(3)と同じパターンなんです。
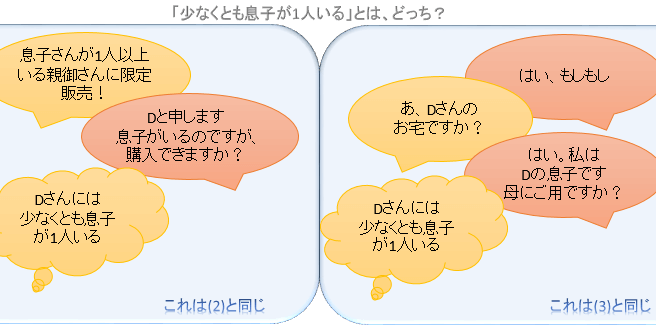
そう、「少なくとも息子が1人いる」という日本語からは、(息子1人・娘1人)の場合に(2)のように100%「息子がいる」と判明する情報取得法だったのか、(3)のように各50%の確率で「息子がいる」「娘がいる」のどちらかが判明する情報取得法だったのか、この問題文だけでは判別できないので、それを聞く必要があるんです。
「どうやってその情報を手に入れたのか」という情報が、事後確率を変動させるのですから。
記載がない以上、数学上はその情報は存在しないものとして2/3と「推定」することにはなりますが、実務的に考えれば、「どうやってその情報を手に入れたのか」という情報が存在しないなら、確率を計算する意味がありません。
よって、実務上は「少なくとも息子が1人だとどうやって判明したのか?」を質問する必要があります。
数学上は2/3と推定できるが、この問題文だけでは不十分。
実務では、どうやってその情報を手に入れたのかを考慮に入れる必要がある。
ベイズ推定による確率的思考は推理力を高める知恵
「なんだこれ。もうワケがわからない!」と思う人もいるかもしれませんが
実はこの計算、皆さんも無意識の間にやっていることなんですよ。
 By: Randen Pederson
By: Randen Pederson例えば…
部長「いやー、うちの子も小学生になってね。子供1人でも結構手がかかるよ」
(お子さんは1人なのか)→男50%女50%
部長「この前もサッカーで怪我をしたみたいだし」
(サッカーで怪我?男の子かな?)→男80%女20%
部長「親としてはもう少し大人しくしてほしいんだけどなぁ。あれじゃ将来結婚できるか心配だよ」
(ん?やんちゃな女の子ってことか?)→男30%女70%
部長「しかし、戦隊モノのオモチャも高いね。友達と一緒に遊ぶんだってせがまれて、大変だよ」
(やんちゃな女の子でも戦隊モノを好きになるのかな。分からなくなってきた)→男65%女35%
部長「でも、やっぱり娘は可愛いもんだね」
(女の子だったか)→女100%
話を聞く前から、部長の子供が男の子か女の子かは確定していて、それぞれ50%の確率のはずなのに、話を聞くにつれてその推理が変動していくのが分かります。
これは、情報量が「あなたの直感的確率」を変動させているのに他なりません。
これを数式できちんと表したのが、ベイズ推定です。
ベイズ推定は、うまく活用することで「直感的確率と実際の確率のズレ」を減らし、推理力を高めるのに便利な知恵です。
ただ、誤解しやすいだけに、注意して使いたいところですね。