回帰分析とは、説明変数 \(x\) によって目的変数 \(y\) の変動を \(y=f(x)\) の形でどの程度説明できるのかを分析する手法です。
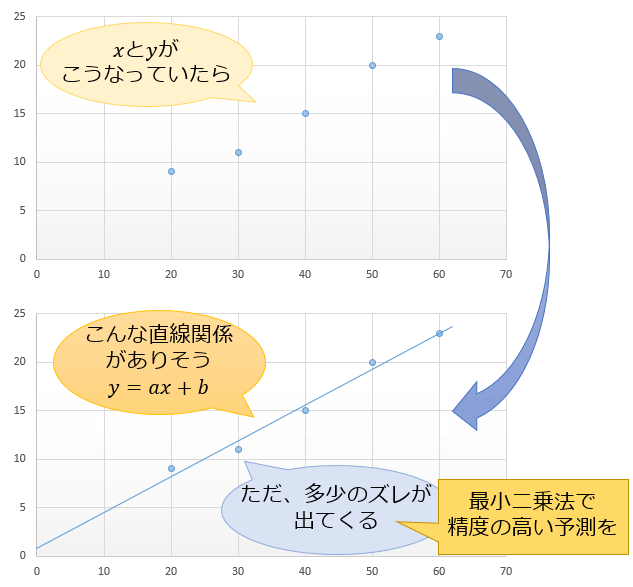
例えば賃貸マンションでは、部屋が広ければ広いほど家賃が高くなる傾向がありますよね。
つまり、部屋の広さを \(x\) 、家賃を \(y\) と考えた場合
2つの変数の間には \(y=ax+b \) という直線関係があると考えられる訳です。
目的変数 \(y\) は従属変数・応答変数とも呼ばれています。
ただ、現実には「同じ部屋の広さなのに家賃に差がある」など、部屋の広さだけでは家賃の変動を説明しきれない「誤差」が出てくるものです。
今回は、この「誤差の推定値(残差)」の2乗和が最小になる直線を計算する、回帰分析の代表的手法「最小二乗法」について軽く説明していきます。
単回帰分析における最小二乗法の公式
最小二乗法による回帰直線(単回帰モデル)は、\(n\)個の2変数データ \((x_i,y_i)(i=1,2,…,n)\)が与えられているときに、以下の公式で表されます。

※単回帰モデル…説明変数が1つしかないもの。「部屋の広さ」だけで家賃を説明したい場合などに使う
※重回帰モデル…説明変数が複数あるもの。「部屋の広さ・築年数・駅からの距離」の3つで家賃を説明したい場合などに使う
なぜこの公式で求められるのかについては、「単回帰分析・最小二乗法の公式はどうすれば求められるのか。統計上の誤差と残差の違い」の記事を参照してください。
手計算とEXCEL計算
今回は、以下の \(No.1~No.5\) の5つの部屋について最小二乗法で回帰直線を求めます。

平均・分散・共分散の公式からささっと計算してしまいましょう。
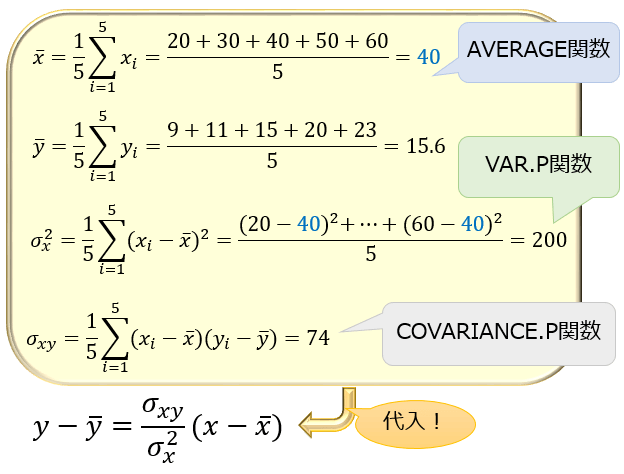
以上から
\(y-15.6=\frac{74}{200}(x-40)\)
⇔ \(y=0.37x+0.8\)
が求まりました。
一度手計算をして計算法が分かったら、それ以降はEXCELで計算すると良いでしょう。
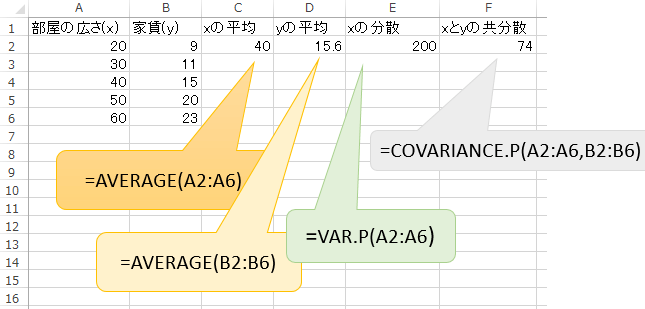
EXCELには最小二乗法を計算してくれるツールもあるので、計算の仕組みを理解した後はこれを使うと便利です。バージョンによりますが、以下はその一例。
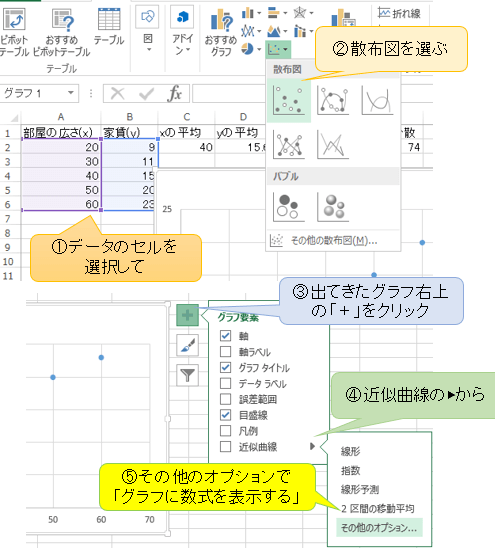
結果、以下のように回帰直線が表示されます。
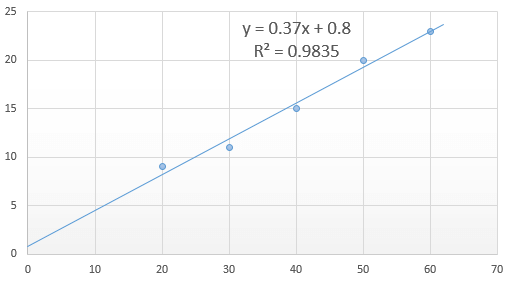
※横軸が \(x\) 縦軸が \(y\)
実際に \(x\) に各 \(x_i\) を代入してみると、対応する \(y_i\) に近い値になっていることが分かりますね。
\(R^2\)は決定係数と言って、説明変数 \(x\) が目的変数 \(y\) の変動をどの程度説明できているかを表しています。
決定係数は \(0\) から \(1\) までの値を取り、 \(1\) に近いほどよく説明できていることを意味します。
公式から分かる回帰直線の性質
また、先の公式をよく見ると、最小二乗法による回帰直線がもつ性質も見えてきます。
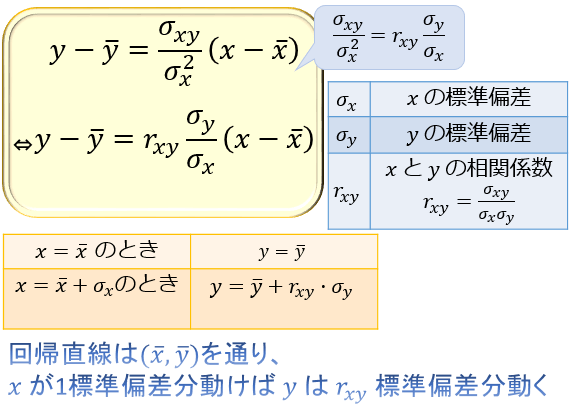
まず1つ目が「回帰直線は\((x_i,y_i)\)の平均である\((\overline{x},\overline{y})\)を通ること」。
2つ目は「説明変数 \(x\) が \(1\) 標準偏差分動くと、目的変数 \(y\) の予測値は \(r_{xy}\) 標準偏差分動くこと」です。
\(r_{xy}\): \(x\) と \(y\) の相関係数。
このように考えると、この公式も覚えやすくなるのではないでしょうか。




