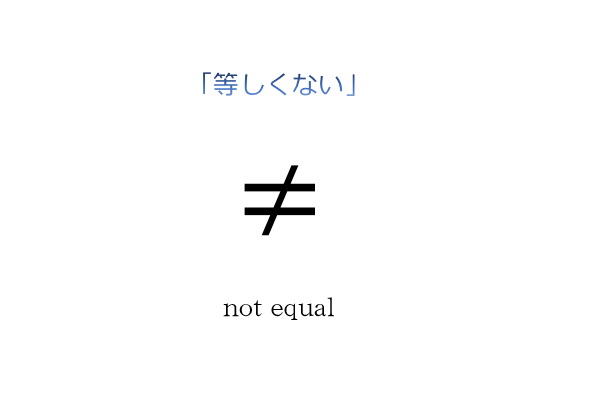エクセルを使って実際に標準偏差を求めようとするときに困るのが、状況によって「標準偏差」という言葉が指す数式が微妙に異なること。
「STDEV.P関数とSTDEV.S関数のどちらを使えばいいのか分からない」「本によって n で割った値の平方根だったり n-1 で割った値の平方根だったりで、どちらが正しいのか分からない」という方も多いのではないでしょうか。
そこで今回は、エクセルで標準偏差を求める2つの関数、STDEV.P関数とSTDEV.S関数の使い分けについて書いていきます。
得られたデータ自体の標準偏差を知りたいときはSTDEV.P
ケース①:5人の身長を計測したところ、以下の結果が得られた。
この5人の身長の標準偏差はいくつか?

このように「得られたデータ(標本)自体の標準偏差を求めたい」場合にはSTDEV.P関数を使って、標本標準偏差 s を求めます。
標準偏差を表示したいセルに、以下のように「=STDEV.P(データ範囲)」を入力してみましょう。
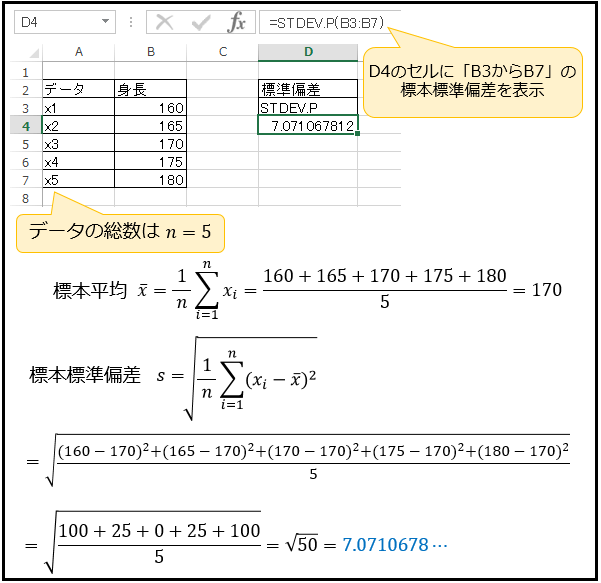
ここから「この5人の身長の標準偏差は約7.07cmである」ということができます。
実際にいちど手計算して、STDEV.P関数で求まった値が正しいかチェックしてみてください。
「5人の身長データを母集団とみなして、母標準偏差 σ を求めている」と説明されることもあります。捉え方が違うだけで計算方法や計算結果は同じです。
得られたデータから母集団の標準偏差を推定したいときはSTDEV.S
ケース②:日本全国から無作為に選ばれた5人の成人男性の身長を計測したところ、以下の結果が得られた。日本にいるすべての成人男性の身長の標準偏差はどのくらいだと推定できるか?

このように「得られたデータ(標本)から、調査の対象となる集合全体(母集団)の標準偏差を推定したい」場合にはSTDEV.S関数を使って、不偏分散平方根 u を求めます。
標準偏差を表示したいセルに、以下のように「=STDEV.S(データ範囲)」を入力してみましょう。
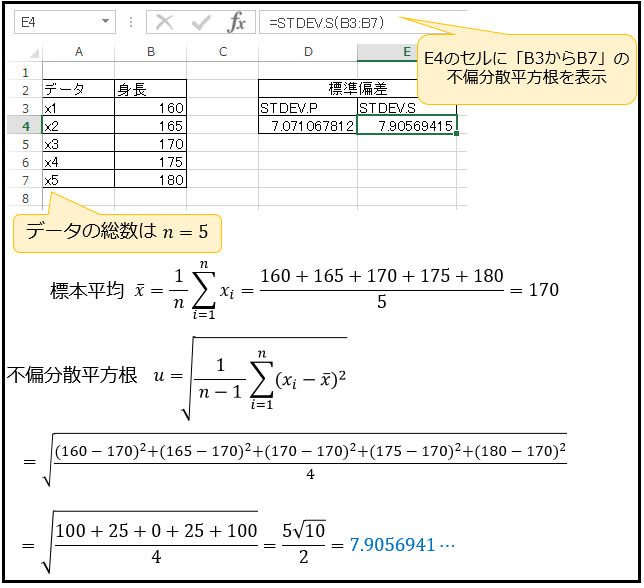
ここから「今回の調査結果では全国の成人男性の身長の標準偏差は約7.91cmと推定される」ということができます。
標本標準偏差 s は「標本自体の標準偏差」を表してはいますが、「母集団の標準偏差」よりもやや小さな値になりやすいという欠点があります。
そのため母集団の標準偏差を推定したい場合には、補正をかけた不偏分散平方根 u を利用したほうが良いのです。
「母集団と標本の関係」や「分母がnでなくn-1になる理由」については「分散や標準偏差において n-1 で割る公式の理由」の記事も参考にしてください。
用語のまとめ
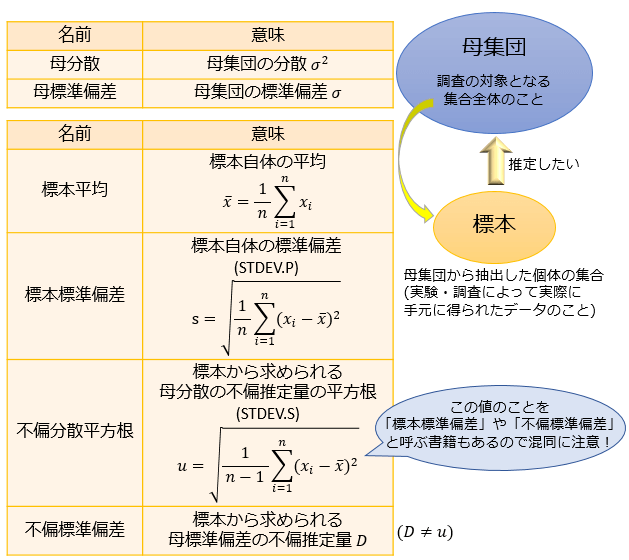
STDEV.S関数で求められる値(n-1で割った値の平方根)は、書籍によって呼び方が異なることがあります。
①不偏分散の平方根としての標準偏差
②標本標準偏差
③不偏標準偏差
この記事では①の呼び方を支持して、不偏分散平方根と記載しています。
というのも、STDEV.S関数で求められる値(n-1で割った値の平方根)は「標本自体の標準偏差」でもなければ「母集団の標準偏差の不偏推定量」でもないからです。
※不偏推定量:その期待値が推定したい値と一致するような統計量のこと。
STDEV.P関数で求められる「標本自体の標準偏差」が標本標準偏差
STDEV.S関数で求められる「母集団の分散の不偏推定量の平方根」が不偏分散平方根
「母集団の標準偏差の不偏推定量」が不偏標準偏差
という定義が一番自然な定義と考えられることから、当サイトではこの定義で記述しています。