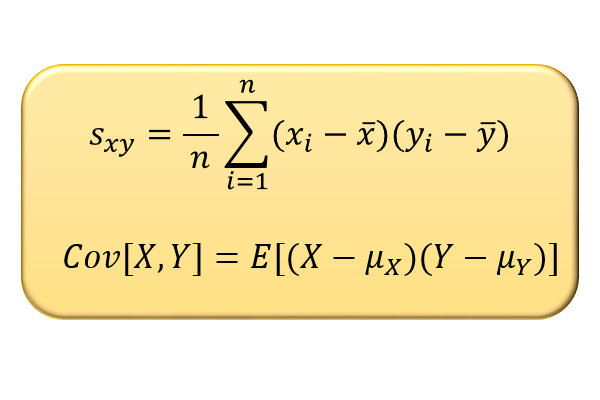離散型の確率変数とは？離散確率分布と確率関数の性質

確率に従って様々な値をとる変数である確率変数は、離散型の確率変数と連続型の確率変数の2種類に分類することができます。

「サイコロの目」のように 1,2,3…ととびとびの値をとるのが、離散型の確率変数。

「ある人の身長」のように小数点以下の値をどこまでも細かくできる(例えば、172cmと一言にいっても、正確には172.0829…cmと無限に続く)のが、連続型の確率変数です。

「当たり前のことだな」と侮られがちですが、この2つの違いをキチンと理解しておかないと意外なところでつまずきやすくなってしまう重要なポイントです。

今回は、離散型の確率変数について見ていきましょう。

photo credit:daBinsi

離散型は、とびとびの値をとる

離散型の確率変数とは、とびとびの値しか取らないものを指します。

例えば、「1日にかかってくる電話の回数」の場合、「1回」の次は「2回」であり、1.4回といった値は取りませんよね。

「サイコロを2回振って出た目の平均」の場合も、「3」の次は「3.5」であり、3.197といった値は取りません。

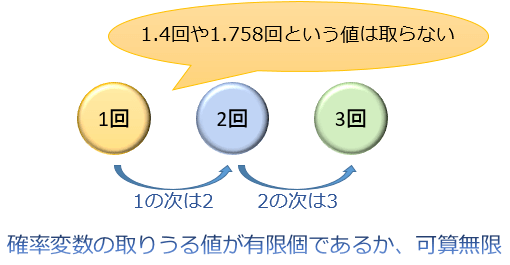
そのため、例えば「1以上6以下」の中で取りうる値の数は

「1日にかかってくる電話の回数」なら{1,2,3,4,5,6}の6個だけですし

「サイコロを2回振って出た目の平均」なら{1,1.5,2,2.5,3,3.5,4,4.5,5,5.5,6}の11個だけです。

連続型の確率変数であれば「1.758や1.000…001や√3」など無限に取りうる値が存在しますが、離散型の場合はそうではないという意味です。

このように、取りうる値が有限個(または無限個であっても可算無限)しかない確率変数。

それが、離散型の確率変数です。

その確率変数が離散型である場合の確率分布を、離散確率分布と言います。

離散確率分布は、確率変数 X の取りうる値 x₁,x₂,…,x_nの1つ1つに対応する確率 P(X=x_i) が存在し、以下の条件を満たします。

P(A)とは、Aという事象が起きる確率のこと。つまり、P(X=x_i)とは確率変数 X が x_iという値をとる確率を意味します。

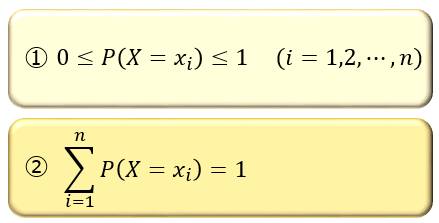
①は、それぞれの値をとる確率は 0 以上 1 以下(0%～100%)である

②は、「全ての事象の確率を合わせれば100%になる」

ということを言っています。

例えば、「偏りのないコインを2回投げて表が出る回数」を確率変数 X とおく場合、以下のようにこの条件を満たしていることが分かります。

取りうる値の個数が少ない時はP(X=x₁)＝△、P(X=x₂)＝□、…と1つずつ書いていっても問題ありませんが、取りうる値の個数が多くなってくると、流石に厳しくなってきますよね。

そんなときは、確率変数 X が x_iという値をとる確率 P(X=x_i) を、f(x_i) という関数で表すと何かと便利です。

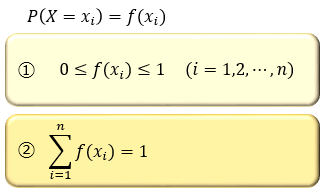
この f(x_i) (i=1,2,…,n)のことを確率関数と呼びます。(確率質量関数とも)

例えば、「偏りのないコインを2回投げて表が出る回数」を確率変数 X とおく場合、その確率関数はこんな式になります。

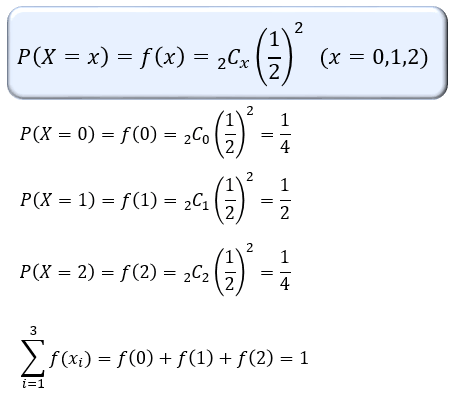
特に、二項分布やポアソン分布の確率関数は見かけることも多いので、ぜひ覚えておきたいところです。