今回は、主な代表値とその強み・弱点について書いていきます。
photo credit:Lucky Lynda
平均値
代表値として最も有名なのが、平均値です。
平均値(算術平均)は、各データの値の合計をデータの総数で割った値です。
エクセルではAVERAGE関数で求められます。

算術平均はすべてのデータからの影響を考慮した値になるので、集団全体の特徴を知るのにとても便利な値です。
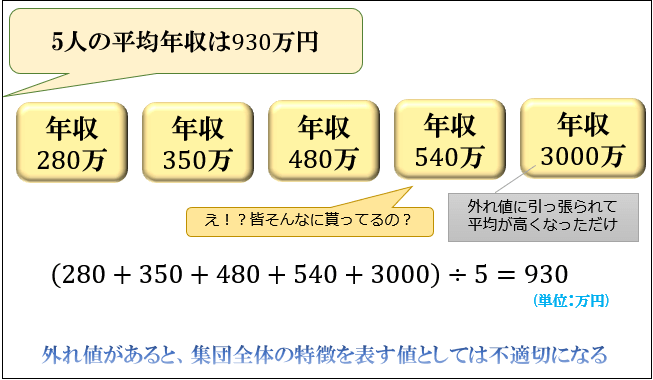
ただし、データの中に他の値から大きく離れた『外れ値』が含まれていると、その影響を大きく受けてしまうという弱点もあります。
中央値
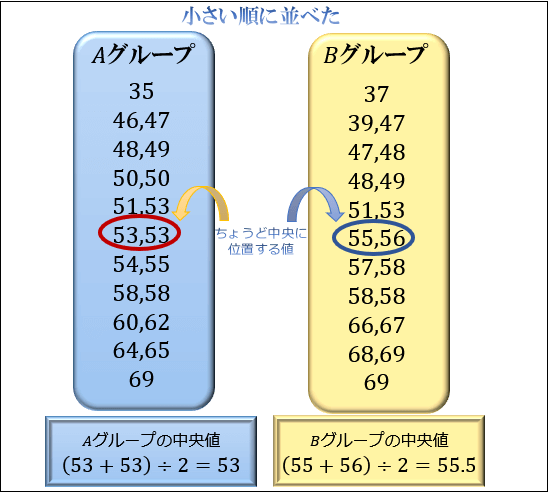
中央値とは、データを小さい順に並べたときにちょうど中央に位置する値のことです。
データの数が偶数個の場合は、中央に位置する2つの値の算術平均をとります。
エクセルでは、MEDIAN関数を使うことで求められます。
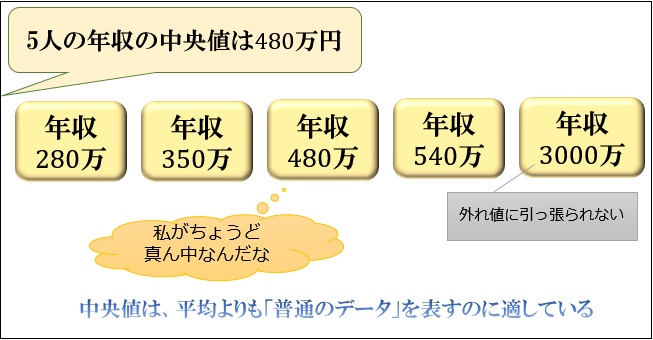
中央値は、平均値と違って外れ値の影響をほとんど受けないため、「普通のデータ」の値を知りたいときは平均よりも中央値の方が適しています。
たとえば、「普通の人はどのくらい給料をもらっているのか?」を知りたい場合は、平均年収よりも年収の中央値を見たほうがいいでしょう。
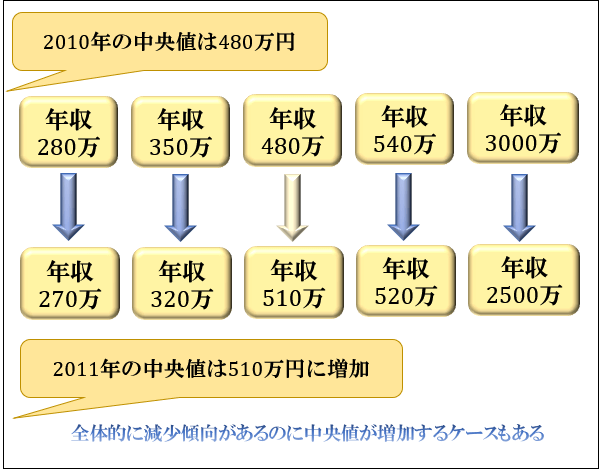
ただし、平均値と違ってすべてのデータからの影響を考慮しているわけではないので、「前年度と比べて全体的に減少傾向があるのに中央値が増加する」というケースもある点に注意が必要です。
中央値はデータの比較にはあまり向いていない、と覚えておきましょう。
最頻値
最頻値とは、データの中で最も頻繁に出現する値のこと。
エクセルではMODE関数で求められる値です。

最頻値は「最も頻繁に出現する値」のみを反映するため、他の値から大きく離れた『外れ値』の影響を受けにくいという強みがあります。
ただし、データの数が少ないと「2回しか出現していない値」が最頻値になるなど、「本当にその集団を代表しているのか?」と疑問に思うような値が選ばれたり、複数の値が最頻値になる可能性がある点に注意が必要です。
最頻値はデータの数が少ない時はあまり役に立たないと覚えておくと良いでしょう。
まとめ
平均値の強み「すべてのデータからの影響を考慮した値になる」
平均値の弱点「外れ値が含まれていると、その影響を大きく受けてしまう」
中央値の強み「外れ値の影響をほとんど受けない」
中央値の弱点「データの比較にはやや不向き」
最頻値の強み「外れ値の影響を受けにくい」
最頻値の弱点「データの数が少ないとあまり役に立たない」
※外れ値:他の値から極端に離れた値のこと
どの代表値にも、それぞれに強みと弱点があります。「そのデータからどんな情報を読み取りたいのか?」を考えながら、適切な代表値を選ぶように心がけたいですね。