今回は、2倍角の公式と半角の公式について書いていきます。
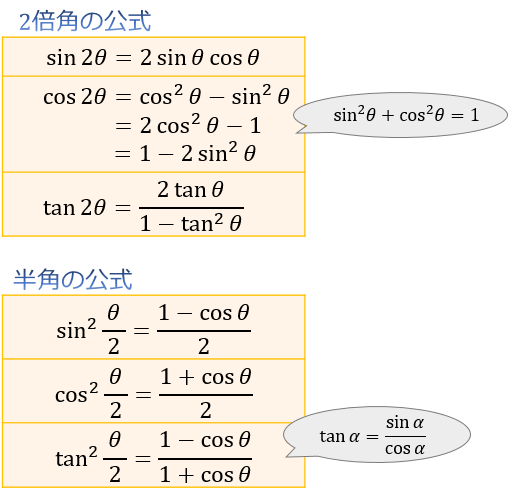
2倍角の公式の証明
2倍角の公式は、加法定理の式に \(α=β=θ\) を代入することで求めることができます。




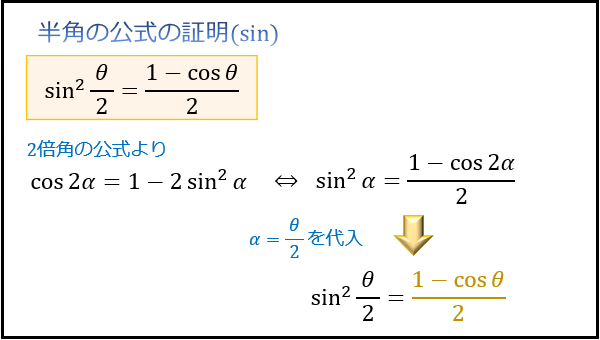
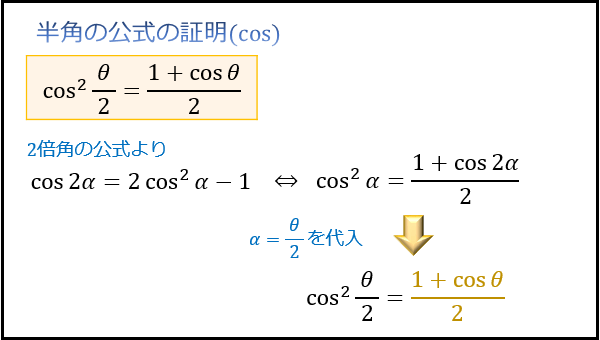
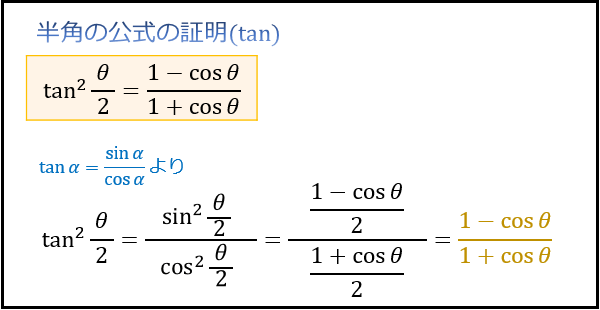
半角の公式の証明
半角の公式は、\(\cos\) の2倍角の公式から求めることができます。
二等辺三角形から分かる2倍角の公式の考え方
2倍角の公式は、\(AB=AC=1\),\(∠CAB=2θ\) の二等辺三角形を考えると分かりやすくなります。
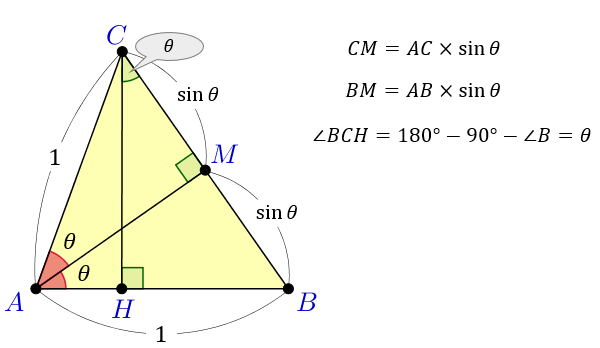
まず、線分 \(CB\) の中点を \(M\) 、点 \(C\) から \(AB\) 上に垂直に下した点を \(H\) とおきます。
すると \(△CAM\) と \(△BAM\) は3辺の長さがすべて同じなので、互いに合同です。
よって \(∠CAM=∠BAM=∠CAB÷2=θ\)
直角三角形 \(CAM\) に注目すると、\(CM=AC×\sin{θ}=\sin{θ}\)
直角三角形 \(BAM\) に注目すると、\(BM=AB×\sin{θ}=\sin{θ}\)
\(CB=CM+BM=\sin{θ}+\sin{θ}=2\sin{θ}\)
と求まります。
次に \(△BAM\) に注目すると、内角の和は \(180°\) より \(∠B=180°-90°-θ=90°-θ\)
今度は \(△BCM\) に注目すると、\(∠BCH=180°-90°-∠B\) \(=90°-(90°-θ)=θ\)
となり、\(∠BCH=∠BAM=θ\) であることが分かります。
\(CB\) の長さと \(∠BCH\) が求まったら、次は下図の青で示した2つの線分 \(CH\) と \(AH\) に注目。
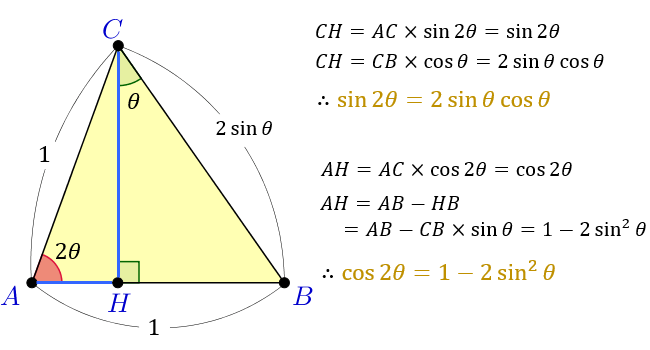
これらは「斜辺の長さ \(1\) ,\(∠CAH=2θ\) の直角三角形 \(CAH\) 」の1辺であることから
\(CH=AC×\sin{2θ}=\sin{2θ}\)
\(AH=AC×\cos{2θ}=\cos{2θ}\)
に対応します。
この \(CH\) と \(AH\) を「斜辺の長さ \(2\sin{θ}\),\(∠BCH=θ\) の直角三角形 \(BCH\) 」から考えると
\(\sin{2θ}=CH=CB×\cos{θ}\) \(=2\sin{θ}\cos{θ}\)
\(\cos{2θ}=AH=AB-HB\) \(=AB-CB×\sin{θ}=1-2\sin^2{θ}\)
と求まり、2倍角の公式を示すことができました。