今回は、条件付き確率とベイズの定理について書いていきます。
条件付き確率とは
ある事象 \(A\) が起こったという条件のもとでの事象 \(B\) の確率 \(P(B|A)\) のことを、「\(A\) を与えたときの \(B\) の条件付き確率」と言います。
\(P(B|A)\) は、\(P_{A}(B)\) と表記されることもあります。
読み方は P B given A(ピーBギブンA)です。
\(P(B|A)\) は、以下の公式から求められます。
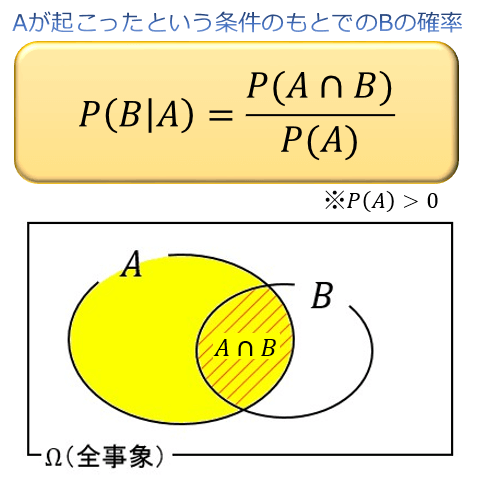
黄色い部分が分母、赤い斜線部が分子です。
条件付き確率の例題
数式だけだとイメージが湧きにくいと思うので、以下の例題を解いてみましょう。
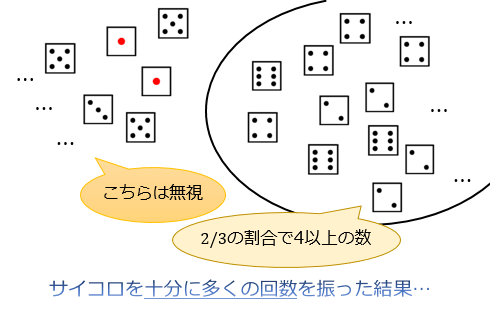
(サイコロの各目の出る確率はそれぞれ \(1/6\) とします)
例題)サイコロを振って偶数の目が出た場合に、それが4以上の目である確率は?
\(A\)「偶数の目が出た」という条件のもとで、 \(B\)「それが4以上の目である」確率 \(P(B|A)\) を求めます。
「偶数の目が出る確率 \(P(A)=1/2\)」「偶数かつ4以上の目(4か6)が出る確率 \(P(A∧B)=1/3\) 」であることから、公式をこのように使います。
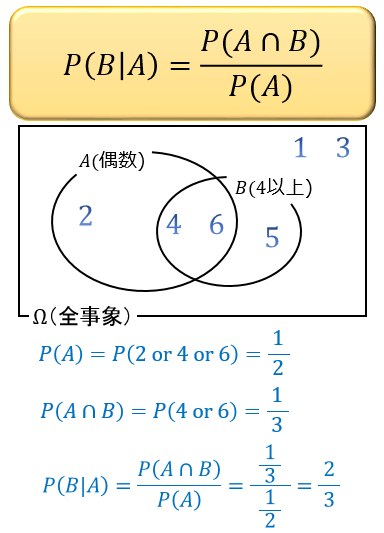
\(P(B|A)=\dfrac{2}{3}\) と求まりました。
ここから「サイコロを振って偶数の目が出たという条件のもとで、それが4以上の目でもある確率」は \(2/3\) であることがわかります。
条件付き確率のイメージがつかめてきたでしょうか?
ベイズの定理とは
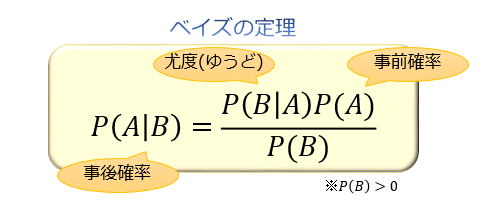
\(P(B|A)\) の逆確率である \(P(A|B)\) は、「\(P(B|A)\) と \(P(A)\) の積を \(P(B)\) で割る」ことで求められる。
これを、ベイズの定理と言います。

「ある事象 \(A\) が起こったという条件のもとでの事象 \(B\) の確率 \(P(B|A)\)」を使って
「ある事象 \(B\) が起こったという条件のもとでの事象 \(A\) の確率 \(P(A|B)\)」を求めよう
というのがベイズの定理の特徴です。
この式において、\(P(A)\) を事前確率・\(P(B|A)\) を尤度・\(P(A|B)\) を事後確率と言います。
条件付き確率の公式を少し式変形しただけなので、「なぜわざわざベイズの定理を習うの?」と疑問に思う方もいるかもしれませんが、この形のほうが応用が利きやすいので、ぜひ覚えておいてください。
ちなみに、ベイズの定理の導出は以下のようになります。

迷惑メールを自動的に発見・分類する知恵

ベイズの定理(条件付き確率)が役に立っている代表例として、迷惑メールを自動的に発見・分類してくれるフィルタリング機能が挙げられます。
例題)過去の調査から、無作為に選んだメールの \(20\) %が迷惑メール、\(80\) %が一般メールだと分かった。
調査によると、迷惑メールが『キャンペーン』という単語を含んでいる確率は \(30\) %、一般メールが『キャンペーン』という単語を含んでいる確率は \(4\) %である。
無作為に選んだメールが『キャンペーン』という単語を含んでいた場合、これが迷惑メールである確率は?
A:迷惑メールである
B:『キャンペーン』という単語を含んでいる
とおいて考えてみましょう。
まず、過去の調査から「無作為に選んだメールが迷惑メールである確率」は \(P(A)=0.2\) だと分かっています。

次に、無作為に選んだメールが『キャンペーン』という単語を含んでいたという条件のもとで、それが迷惑メールである確率を求めます。
迷惑メールが『キャンペーン』という単語を含んでいる確率は \(30\) %
一般メールが『キャンペーン』という単語を含んでいる確率は \(4\) %
という情報を反映させてみましょう。

迷惑メール(\(0.2\))という条件の下で『キャンペーン』という単語を含んでいる確率は \(0.3\) なので、「迷惑メールかつキャンペーンという単語を含んでいる確率」は \(0.2×0.3\)
一般メール(\(0.8\))という条件の下で『キャンペーン』という単語を含んでいる確率は \(0.04\) なので、「一般メールかつキャンペーンという単語を含んでいる確率」は \(0.8×0.04\)
となります。
この図から、「無作為に選んだメールがキャンペーンという単語を含んでいる確率」は
\(P(B)=0.2×0.3+0.8×0.04=0.092\) だと分かります。(図の黄色い部分に相当)
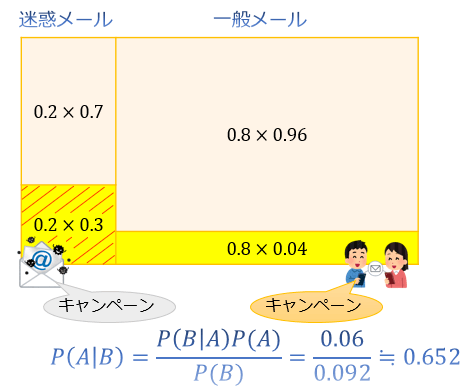
あとは、黄色い部分を分母、赤い斜線部を分子にとることで「無作為に選んだメールが『キャンペーン』という単語を含んでいたという条件のもとで、それが迷惑メールである確率」は \(P(A|B)≒0.652\) と求まります。
事前確率 \(P(A)=0.2\)、尤度 \(P(B|A)=0.3\)、\(P(B)=0.092\)
事後確率 \(P(A|B)=0.2×0.3/0.092≒0.652\)
このように『キャンペーン』という単語を含んでいたことに着目することで、それが迷惑メールである可能性が \(20\) %から約 \(65.2\) %、実に3倍にまで高まったことが示されました。
これを、ベイズ更新と言います。