連立方程式とは、同時に成立する2つ以上の方程式のこと。
複数の制約条件を同時に満たす解を求める手法です。
物理・経済・統計・会計、どんな分野でも連立方程式をさけて通ることはできません。
「限られた資源の中で、多くの制約条件を同時にクリアできる最適解を見つけ出す」ことは、すべての分野に共通する普遍的な課題だからです。
今回は、そんな連立方程式の解き方について軽く解説していきます。
photo credit:Enrico
連立方程式の解法(加減法)
例題)
りんご2個とみかん5個を買うには180円必要です。
りんご3個とみかん4個を買うには200円必要です。
りんごとみかんは、1個あたりそれぞれ何円でしょうか?
りんご1個を x 円、みかん1個を y 円とおくと以下の連立方程式が成立します。
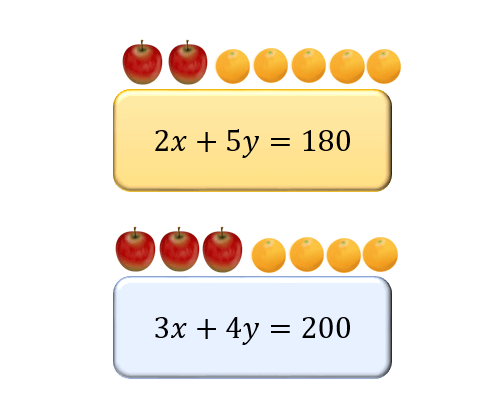
step① 2つの式を数倍して、係数をそろえる
まず、xかyどちらかの係数をそろえます。今回は、xの係数をそろえてみましょう。
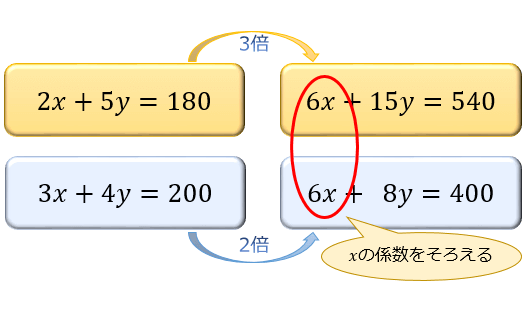
xの係数が6でそろいました。
step② 1つ目の式から2つ目の式を引き、yを求める
xの係数をそろえたら、1つ目の式から2つ目の式を引きます。
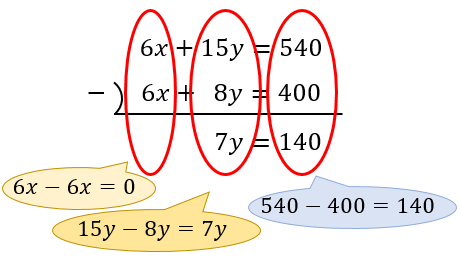
2つの方程式をたてに並べて、引き算していきましょう。
すると、7y=140が求まるので、後はこの式の両辺を7で割ればy=20が求まります。
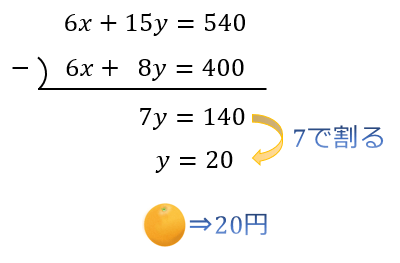
step③ yを代入して、xを求める
最後に、初めの式に y=20を代入すれば 2x=80から、x=40が求まります。

以上から、x=40 y=20がこの連立方程式の解となります。
Tooda Yuuto
ここから、りんごが40円でみかんが20円だと分かります。
なぜ加減法が成り立つか
加減法は、2つの式の共通点を抜き出すことによって
「りんごとみかん」の式を「みかん」だけの式に変換する手法です。
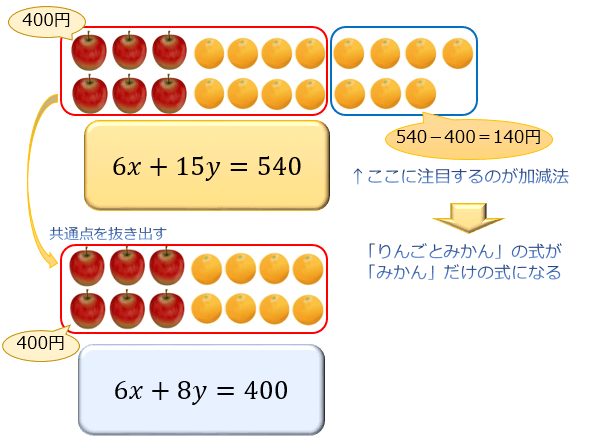
係数をそろえてから2つの差を取ることで、2次式を1次式へと「次元を1つ落としている」ので簡単に計算できるようになります。
Tooda Yuuto
「共通点を抜き出すことで次元を1つ落とす」テクニックは、色んな分野でよく使う手法なので、ぜひ覚えておいてください。