例題)「30%の確率で100円、50%の確率で300円、20%の確率で800円もらえる」というゲームがあるとする。このゲームでもらえる金額の期待値はいくらか?

期待値とは、「確率を考慮した平均」です。
期待値の求め方
Step①確率分布表を作る
まず、「取りうる値」と「その値を取る確率」を対応させた表を作ります。
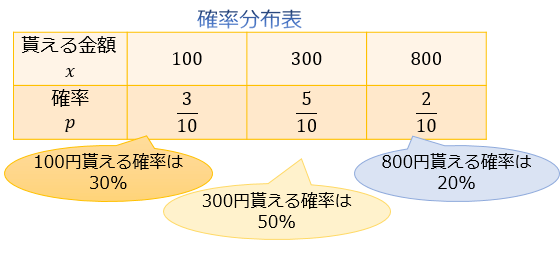
この表のことを、確率分布表と言います。
Step②「値」と「確率」をかけ算する
次に、「取りうる値」と「その値をとる確率」をそれぞれかけ算して、積を求めます。
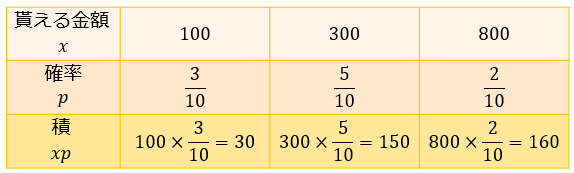
※積:かけ算した結果のこと。2と3の積は6。
Step③それらを合計すると期待値が求まる
最後に、求まった積をすべて合計すると、期待値が求まります。

このゲームでは、1回あたり平均して340円もらえることが分かりました。
今回は、この期待値の定義・公式・注意点について書いていきます。
photo credit:Saranya Chawanrattanasakul
期待値の定義・省略表記
期待値は、確率変数 X の「取りうる値 x1,x2,…,xn」と「その値をとる確率 p1,p2,…,pn」の積の合計として求められる値です。

期待値は英語で Expected Value という事から、省略してEVと表記されることもあります。
数式では、 E[X] で「確率変数 X の期待値」を意味します。
P(X=xi) は「確率変数 X が xi の値をとる確率」を意味しています。
期待値の公式
期待値についておさえておくべき公式は以下の6つ。
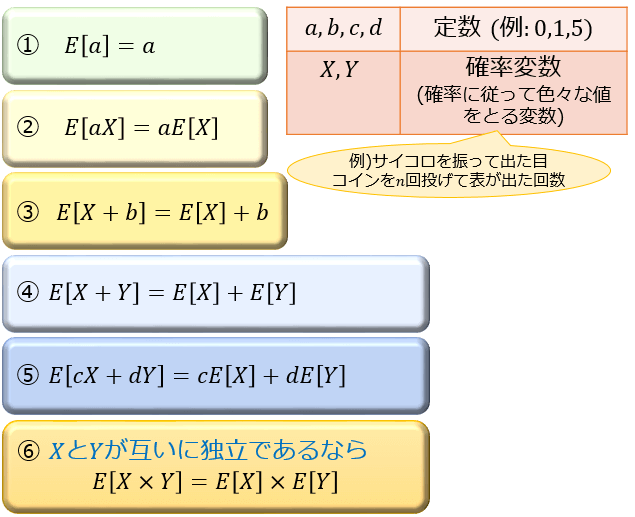
①は、「定数 a は100%の確率で a となる値」と考えるとイメージしやすいと思います。
<独立の意味>

十分な回数をこなせる場合の目安
期待値は「確率に従って色々な値をとる変数が、平均的にどのくらいの値をとるのか?」を考えるのに便利な値です。
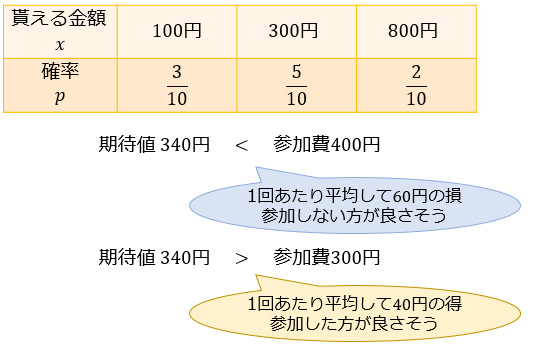
たとえば初めに述べた例題のゲームなら、期待値が340円なので
参加費が1回400円の場合は「何回も参加すれば平均的には損していく」ことが分かりますし
参加費が1回300円の場合は「何回も参加すれば平均的には得していく」ことが分かります。
ただし、ここで注意してほしいのが「期待値を目安にしていいのは、十分な回数試行できる場合だけ」であること。
「サイコロを6回投げても、1から6の目がすべて1回ずつ出るとは限らない」ように、確率というのは多少はばらつきが出るものです。
そのため、試行回数が少ない場合は期待値から大きく離れた結果になるケースも珍しくないんです。
【20%の確率で510万円もらえる、参加費100万円のゲームの場合】

「ほんの数回しか試せないもの」なのであれば、期待値を目安に考えるべきではないことを覚えておいてください。
例)HP700の相手に「①威力200・命中率100%」の剣と「②威力260・命中率80%」の斧のどちらで挑むべきか?⇒剣なら4回命中・斧なら3回命中で倒せる。試行回数が少ないので、期待値よりも確率分布を考えた方が良い。
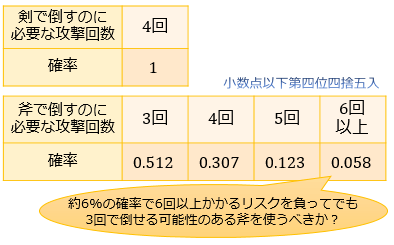
※確率の算出は二項分布の記事を参考
「どの程度ばらつくものなのか」を表わす指標である分散と組み合わせて使うことで、一気に活用の幅が広がる値です。