
今回は、連続型の確率変数について書いていきます。
離散型の確率変数:「サイコロの目」のように 1,2,3…ととびとびの値をとる
連続型の確率変数:「ある人の身長」のように小数点以下の値をどこまでも細かくできる
前回取り上げた離散型の確率変数は高校数学でも出てくる身近な考え方である一方、今回紹介する連続型の確率変数は微分・積分の知識を使うので、計算が少々ややこしくなります。
「離散型の確率変数とは?離散確率分布と確率関数の性質」の記事とあわせて、その違いを意識しつつ読んでみてください。
photo credit:Fabrizio Russo
連続型は、ある区間内のすべての実数をとる
連続型の確率変数とは、時間・温度・身長などの連続的な値(実数値)をとるものを指します。
 By: Michael Pollak
By: Michael Pollak
例えば、「ある人の身長」の場合、172cmと一言にいってもピッタリ172.0000cmという人はまずいませんよね。
より正確に計測すれば、172.0829cmといったようにジャスト172cmとは微妙に異なる値をとるはずです。
さらに正確に計測すれば、172.08296876…cmとどこまででも細かくしていけるので、同じ「172cm台の人」をどれだけ集めても、その正確な値は無限通り存在し、「1人として完全に同じ身長の人はいない」ことが分かります。

つまり、身長の「172cm」と「173cm」の間だけ見ても取りうる値が無限(それも非可算無限)に存在するわけです。
そのため、仮に「次にお店に入って来る人の身長」を確率変数 X と置いた場合、Xはある区間内(たとえば130以上200以下)のすべての実数を取りうることになります。
このように、取りうる値が「ある区間内のすべての実数」である確率変数。
それが、連続型の確率変数です。
連続確率分布
その確率変数が連続型である場合の確率分布を、連続確率分布と言います。
連続確率分布は、a<bとなる任意の実数a,bについて、以下の条件を満たします。

①は、ある特定の値をピッタリと取る確率は 0 であるということを意味します。
例えば、「次にお店に入って来る人の身長がピッタリ172.0000…cm」という事はまずありませんよね。
このように、連続型の確率変数は小数点以下の値をどこまでも細かくできてしまうので、その反面「特定の一点の値をピッタリと取る確率」は0になってしまうのです。
連続確率分布では、「次にお店に入って来る人の身長が172cm以上173cm以下である確率」といったように「区間」に対して確率が求められます。
これを表しているのが②。
a<bとなる任意の実数a,bに対して、確率変数 X が区間「 a 以上 b 以下」の値を取る確率は 0 以上 1 以下(0%~100%)となります。
③は確率の公理で、「全ての事象の確率を合わせれば100%になる」という意味です。
離散確率分布:「取りうる値1つ1つ」について確率が求められる
連続確率分布: a 以上 b 以下といったように「区間」についてのみ確率が求められる
確率密度関数
連続確率分布では区間についてのみ確率が求められるので、離散確率分布のように確率関数 f(xi)=P(X=xi) を定義することができません。
代わりに定義されるのが、確率密度関数です。
確率密度関数とは、確率変数 X が区間「 a 以上 b 以下」の値を取る確率 P(a≤X≤b) に対して、以下のように積分の形で表される関数 f(x) を指します。
簡単にいうと「どういった結果がどのくらい起こりやすいのか」を表す関数です。

例えば、「0以上100以下の無限に存在する実数の中からランダムに1つ選ばれる一様乱数(選ばれる確率がどれも等しい)」を確率変数 X とおく場合、Xの確率密度関数は以下の式で与えられます。
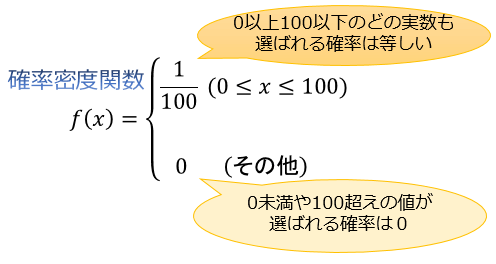
この確率密度関数 f(x) をグラフで表したのが、下図の赤線です。
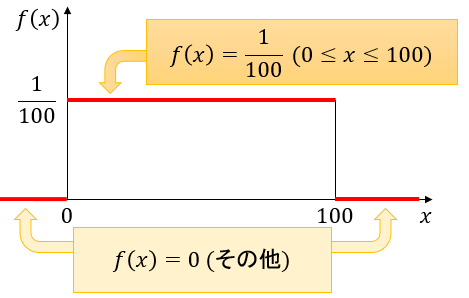
連続確率分布では、確率はこの確率密度関数と横軸(x軸)で囲まれた部分の面積で表されます。
例えば確率変数 X が30以上55以下の実数(47.793…など)を取る確率は、下の青い部分の面積に相当します。
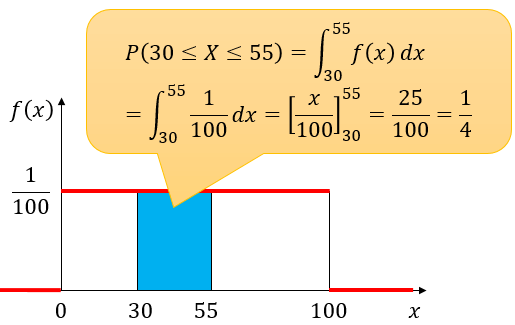
また、以下のようにこの確率密度関数が「全ての事象の確率を合わせれば100%になる」という確率の公理を満たしていることも分かります。
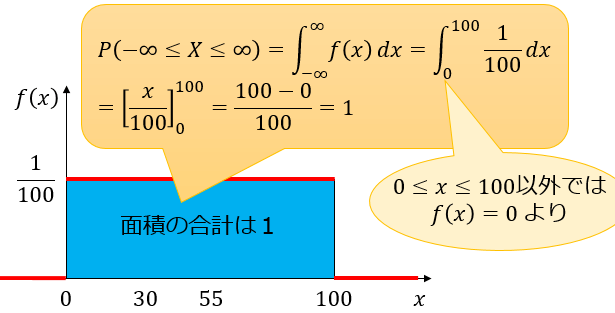
連続型の確率変数において a 以上 b 以下の値を取る確率は、その面積によって求められます。
そう考えると、「横の長さが 0 の図形の面積は 0 」ですから、特定の一点の値をピッタリと取る確率が0になるのも分かりやすいですね。





