いま、「1」「2」「3」「4」「5」の5枚のカードがあるとします。
この5枚のカードについて、2種類の問題を考えてみましょう。
①:「この中から2枚を使って2ケタの数字を作る場合、作れる数字は何通りあるか?」
②:「この中から2枚のカードを選ぶ場合、選び方は何通りあるか?」

この2種類の問題では、それぞれ答えが変わってきます。
①は順列で、答えは 5P2=5×4=20通り
②は組み合わせで、答えは 5C2=5×4÷2=10通りになります。
今回は、そんな順列と組み合わせの数の考え方についてです。
photo credit:William Warby
①順列
異なるn個の中から k 個を順番をつけて並べる場合の並べ方は nPk で表され、順列の公式から求められます。

「!」は階乗(かいじょう)と言って、n から 1 までのすべての整数をかけ算した値のことを n! と表記します。(ただし、0!=1と定義される)
たとえば、 7! は 7×6×5×4×3×2×1=5040 を意味します。
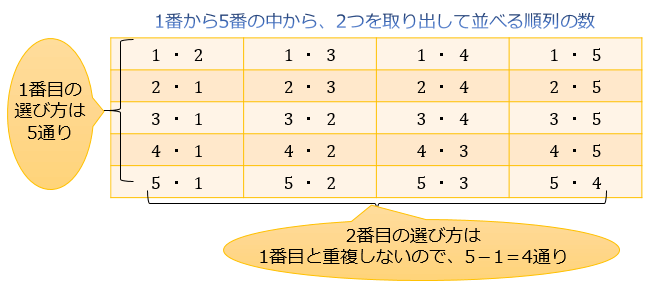
初めにあげた「1」「2」「3」「4」「5」の5枚で作れる2ケタの数は
(12,13,14,15,21,23,24,25,31,32,
34,35,41,42,43,45,51,52,53,54)の20通り
これは、この順列の公式を使う事で
5P2=5×4=20通り
と求めることができます。
下のように表にして考えると、順列が 5×4=20 になるのが分かりやすいです。
「1」「2」「3」「4」「5」「6」の6枚のカードで作れる4ケタの数の場合は
6P4=6×5×4×3=360通りとなります。
②組み合わせ
一方、異なるn個の中から k 個を順番をつけずに選ぶ場合の選び方は nCk で表され、組み合わせの数の公式から求められます。

組み合わせの数(nCk)は、ちょうど順列の数(nPk)を k! で割った値になります。
これは、順列では「並びだけが違う、組み合わせとして見たら同じものが1セットにつき k! 個ずつ存在する」のが理由です。

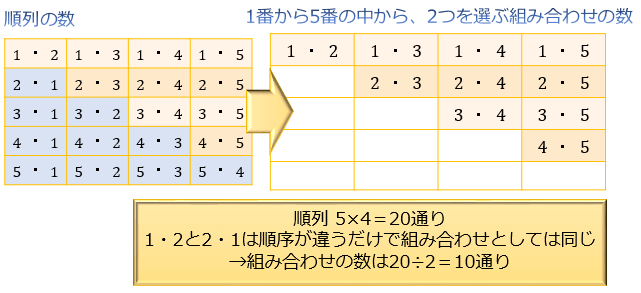
初めにあげた「1」「2」「3」「4」「5」の5枚から2枚を選ぶときの選び方は
(12,13,14,15,23,24,25,34,35,45)の10通り
これは、この組み合わせの数の公式を使う事で
5C2=5×4÷2=10通り
と求めることができます。
下のように表にして考えると「並びだけが違う、組み合わせとして見たら同じものが1セットにつき 2!=2 個ずつ存在する」のが分かりやすくなります。
「1」「2」「3」「4」「5」「6」の6枚から4枚を選ぶ組み合わせの数の場合は
6C4=(6×5×4×3)÷(4×3×2×1)=15通りとなります。
順列か?組み合わせか?の判断テクニック
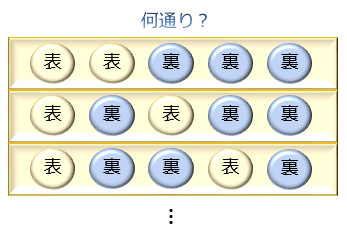
では、ここで問題です。
「コインを5回投げたうち、表が2回出るパターンは何通り?」
この問題では、順列と組み合わせ、どちらの公式を使うべきでしょうか。
 By: frankieleon
By: frankieleon
正解は、組み合わせの数の公式。答えは 5C2=10通りとなります。
この性質から、組み合わせの数は「コインを5回投げたときに2回表が出る確率」を求めるときなどに、二項分布の確率関数で利用されています。

「どちらの公式を使うべきか少し迷った」という方も多いのではないでしょうか?
このように、順列と組み合わせ、どちらの公式を使うべきか悩んだときに役に立つのが
「順番を並べかえたときに意味が変わるか?」で考えるテクニックです。
順番を並べかえたときに意味が変わる・・・順列
順番を並べかえても意味が変わらない・・・組み合わせ
たとえば、『5色の中から重複せずにカーテンとベッドの色を選ぶときの選び方』は
「青のカーテン+白のベッド」と「白のカーテン+青のベッド」では意味が変わるので、順列
一方、コイン投げは「1回目と4回目に表が出る」と「4回目と1回目に表が出る」では意味が変わらないので、組み合わせ
といった具合です。
①:2ケタの数「14」と「41」では意味が変わるので順列
②:「1と4を選ぶ」と「4と1を選ぶ」では意味が変わらないので組み合わせ